The a Derivatives (CXa, CZa, CmJ

The a derivatives describe the changes that take place in the forces and moments when the angle of attack of the airplane is increased. They are normally an increase in the lift, an increase in the drag, and a negative pitching moment. The contents of Chap. 2 are relevant to these derivatives.

‘Since X and Z are the aerodynamic forces acting on the airplane, there are no weight components in

(5.1,1) .

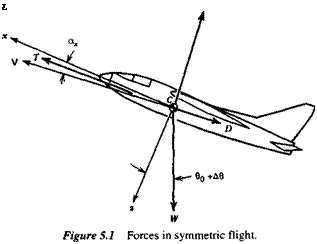THE DERIVATIVE CXa

By definition, CXa = (ЭСх/Эа)0, where the subscript zero indicates that the derivative is evaluated when the disturbance quantities are zero. From (5.1,1)

dCx dCT dCL dCD

da da L x da da

We may assume that the thrust coefficient is sensibly independent of ax so that dCT/da = 0, and hence

where the subscript zero again indicates the reference flight condition, in which, with stability axes, ax = 0. When the drag is given by a parabolic polar in the form CD = Cn + Cj/тгАе, then

b’min l – 7

ЭCD _ 2CU. C’ Эа )0 7тАе ‘

THE DERIVATIVE CZa

By definition, CZa = (dCJda)0. From (5.1,1) we get

Therefore

cza= ~(CLa + CDo) (5.2,3)

CDo will frequently be negligible compared to CLa, and consequently CZa = — CLa.

THE DERIVATIVE C,„

a

Cma is the static stability derivative, which was treated at some length in Chap. 2. It is conveniently expressed in terms of the stick-fixed neutral point (2.3,25):

Cm,, = Ф ~ hn)

For airplanes with positive pitch stiffness, h<hn, and Cma is negative.