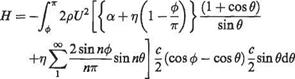The hinge moment coefficient

A flapped-aerofoil characteristic that is of great importance in stability and control
calculations, is the aerodynamic moment about the hinge line, shown as Я in Fig. 4.16.
Taking moments of elementary pressures p, acting on the flap about the hinge,

where p — pUk and xf = x — (1 — F)c. Putting

c c c

xf = – (1 – cos 9) — – (1 — cos ф) = – (cos ф – cos 9)

and к from Eqn (4.51):

Substituting Я = Ch ^pU2(Fc)2 and cancelling

(4.54)

where

7i = (1 + cos 9) d9 = 7Г — ф — sin ф H ^4

From Eqn (4.54):

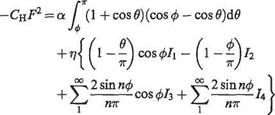
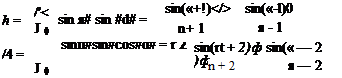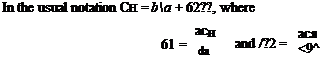1

b=–p; (1 + cos 0) (cos 0 – cos0)d#

J Ф

giving

b — — тто {2(7г – 0)(2cos0 – 1) + 4 sin ф – sin 2ф} 4 Fl

Similarly from Eqn (4.54)

bi = x соетсіеп1 °f V in Eqn (4.54)

This somewhat unwieldy expression reduces to[16]

The parameter a = dC^/da is 2тг and «2 = dCt/ch) from Eqn (4.52) becomes

«2 = 2(7г – ф + sin ф) (4-57)

Thus thin aerofoil theory provides an estimate of all the parameters of a flapped aerofoil.

Note that aspect-ratio corrections have not been included in this analysis which is essentially two-dimensional. Following the conclusions of the finite wing theory in Chapter 5, the parameters a, «2, b and 62 may be suitably corrected for end effects. In practice, however, they are always determined from computational studies and wind-tunnel tests and confirmed by flight tests.