The NACA four-digit wing sections

According to Abbott and von Doenhoff when the NACA four-digit wing sections were first derived in 1932, it was found that the thickness distributions of efficient
wing sections such as the Gottingen 398 and the Clark Y were nearly the same when the maximum thicknesses were set equal to the same value. The thickness distribution for the NACA four-digit sections was selected to correspond closely to those for these earlier wing sections and is given by the following equation:

yt = ±5сф.2969у/1 – 0.1260£ – 0.3516£2 + 0.2843£3 – 0.1015^] (4.84)

where / is the maximum thickness expressed as a fraction of the chord and £ = xjc. The leading-edge radius is

rt = 1.1019c/2

It will be noted from Eqns (4.84) and (4.85) that the ordinate at any point is directly proportional to the thickness ratio and that the leading-edge radius varies as the square of the thickness ratio.

In order to study systematically the effect of variation in the amount of camber and the shape of the camber line, the shapes of the camber lines were expressed analytically as two parabolic arcs tangent at the position of the maximum camber­line ordinate. The equations used to define the camber line are:

Jc = -^2-(2/>£-£2) £<P

Ус = —’2-Id ~2P) + Ы-£2] Z>P (i – P)

where m is the maximum value of yc expressed as a fraction of the chord c, and p is the value of xjc corresponding to this maximum.

The numbering system for the NACA four-digit wing sections is based on the section geometry. The first integer equals ЮОте, the second equals 10p, and the final two taken together equal 100/. Thus the NACA 4412 wing section has 4 per cent camber at x = 0.4c from the leading edge and is 12 per cent thick.

To determine the lifting characteristics using thin-aerofoil theory the camber-line slope has to be expressed as a Fourier series. Differentiating Eqn (4.86) with respect to x gives

dyc __ dpc/c) _ 2m dx d£ p2

Changing variables from І to в where £ = (1 – cos &)j2 gives

= ~ (2p — 1 + cos в) в>в,

dx (l-p)2K J ~ 1

where ep is the value of в corresponding to x = pc.

Substituting Eqn (4.87) into Eqn (4.41) gives xj0 ax

1 f^p YYl 1 fЖ ЇУІ

= -/ —={2p — 1 + cos0)d0 + – ——— ~ (2p – 1 + cos в) йв

Wo P1 W^(i-p)

= ^[(^- 1)gf, + singf,] + 7r(i-j>)2 ^2P~ 1)(7r~gp)~sin^ (4-88)

Similarily from Eqn (4.42)

A = -/^cos0d0 xJo ax

2»j f ^p 0/И f ^

——=■ / {2p — I)cos0 + cos201d0-|——— = [O-p-I)cos0 + cos201d0

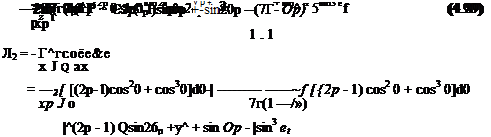T^rJ 0 7г( 1 — P) J 9„

Example 4.2 The NACA 4412 wing section

For a NACA 4412 wing section m = 0.04 and p = 0.4 so that

9P = cos-1 (1 – 2 x 0.4) = 78.46° = 1.3694 rad making these substitutions into Eqns (4.88) to (4.90) gives

A0 = 0.0090, Ai = 0.163 and A2 = 0.0228 Thus Eqns (4.43) and (4.47) give

CL = x(Ai- 2A0) + 2тга = тг(0.163 – 2 x 0.009) + 2тга = 0.456 + 6.2832a (4.91)

Смиі = ~(A1-A2) = -^(0.163-0.0228) = -0.110 (4.92)

In Section 4.10 (Fig. 4.26), the predictions of thin-aerofoil theory, as embodied in Eqns (4.91) and (4.92), are compared with accurate numerical solutions and experimental data. It can be seen that the predictions of thin-aerofoil theory are in satisfactory agreement with the accurate numerical results, especially bearing in mind the considerable discrepancy between the latter and the experimental data.