The Starting Vortex: Kelvin’s Theorem

The existence of circulation around an airfoil may be confirmed by using an inviscid – flow model and Kelvin’s Theorem.[21] The argument is based on the experimental evi­dence of a starting vortex at the trailing edge of an airfoil.

Consider a large closed path, A-B-C-D, enclosing a fixed airfoil in a flow at rest. The circulation around this closed path is zero because the velocity is zero every­where. Assume that the fluid particles comprising this path were marked in some way and then impulsively set the flow in motion from rest. Kelvin’s Theorem states that for an inviscid flow, the time rate of change of circulation around a closed path comprised of the same fluid particles is zero. That is: in Eulerian derivative notation. This means that the circulation that was initially zero around the original closed path, A-B-C-D, must continue to be zero even when the closed path is swept downstream because A-B-C-D always is assumed to be described by the same fluid particles.

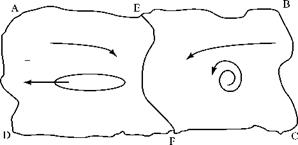
Now, assume that the flow continues at a constant velocity and that a starting vortex was formed and shed. Let the time interval dt be short enough and the closed path be large enough so that both the airfoil and the shed vortex are contained within A-B-C-D, as shown in the snapshot taken at t = dt (Fig. 4.17). Remember that the circulation around this closed path is still zero.

Figure 4.17. The starting vortex.

Now, subdivide the original closed path, A-B-C-D, into two parts by adding an arbi­trary line, E-F, located somewhere between the airfoil and the shed vortex. Around the closed path E-B-C-F, there is a nonzero value of circulation because the path encloses a vortex. However, this means that an equal and opposite circulation must exist around A-E-F-D because the sum of the two must cancel to satisfy Kelvin’s Theorem. Because the starting vortex was formed when the flow along the lower surface of the airfoil tried to go around the trailing edge and then separated, the sense of the starting vortex is counterclockwise for positive lift. The conclusions, then, are that a circulation must be present around the airfoil, it must have a unique value, and it must have a clockwise sense.

4.7 Summary

In this chapter, we introduce techniques for solving aerodynamics problems involving incompressible, inviscid flow fields. We demonstrate that under these con­ditions, the governing equations reduce to the Laplace’s Equation, which has been studied extensively in many fields. Because it is a linear differential equation, its simplest solutions can be superimposed to produce more complex flows. We carry out solutions for four cases that we identify as the uniform flow, the simple source (or sink), the vortex, and the doublet. Superposition of a uniform freestream with a doublet and a vortex yields a solution that we identify as the flow around a spinning cylinder. Of great significance in this example is the creation of lift. This enables us to search for the fluid-dynamics origin of the lifting force, which we identify as the generation of a circulatory flow around the moving body. This idea is extended in the form of the Kutta-Joukouski Theorem to represent the lift on bodies of arbitrary shape. The need for a sharp trailing edge in creating lift on an airfoil is discussed, and the results are summarized in the so-called Kutta condition.