The thickness problem for thin aerofoils

A symmetrical closed contour of small thickness-chord ratio may be obtained from a distribution of sources, and sinks, confined to the chord and immersed in a uniform undisturbed stream parallel to the chord. The typical model is shown in Fig. 4.21 where a(x) is the chordwise source distribution. It will be recalled that a system of discrete sources and sinks in a stream may result in a closed streamline.

Consider the influence of the sources in the element 6xi of chord, X from the origin. The strength of these sources is

6m = a{x)6x

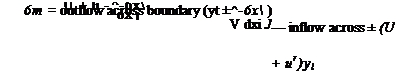Since the elements of upper and lower surface are impermeable, the strength of the sources between *i and *i + &ci are found from continuity as:

Neglecting second-order quantities,

6m = 2и^^-6х

QXl

The velocity potential at a general point P for a source of this strength is given by (see Eqn (3.6))

6ф = —In r

= -^<5*,lnr (4.97)

‘K d*i

where r = у (x — X])2 +y2. The velocity potential for the complete distribution of sources lying between 0 and c on the jc axis becomes

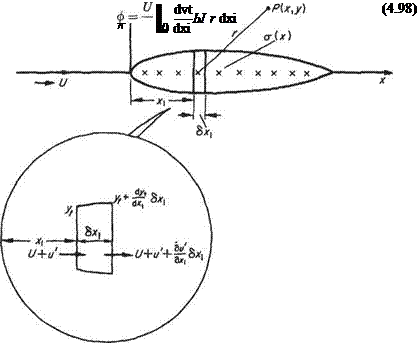Fig. 4.21

and adding the free stream gives

Differentiating to find the velocity components

дф TJ U fcdyt (x-Xi) dx ‘KjQdx(x-xly+y1 = дф^и rcdyt у

dy ‘xJo dxi (x — x])2 + y2 1

To obtain the tangential velocity at the surface of the aerofoil the limit as у —► 0 is taken for Eqn (4.100) so that

M= U + u’ = U + – f^—^—dxi (4.102)

irJo dxi x — xi

The coefficient of pressure is then given by

„ „и’ 2 rcdyt 1 ,

The theory in the form given above is of limited usefulness for practical aerofoil sections because most of these have rounded leading edges. At a rounded leading edge djt/dxi becomes infinite thereby violating the assumptions made to develop the thin-aerofoil theory. In fact from Example 4.3 given below it will be seen that the theory even breaks down when dyt/djti is finite at the leading and trailing edges. There are various refinements of the theory that partially overcome this problem[18] and others that permit its extension to moderately thick aerofoilsЛ

Example 4.3 Find the pressure distribution on the bi-convex aerofoil

2"

(with origin at mid-chord) set at zero incidence in an otherwise undisturbed stream. For the given aerofoil

Уі = ±

c 2c

and

= —4r— dxi c2

From above:

, и fc/1 t Xi и = — /—– —4-^ dxj

KJ-c/2 CZX~X 1

or

2 4f Г0/2 x,

= ~~3 —— d*i

C2 J_c/2 X – Xi

Thus

At the mid-chord point:

x = 0 C„ =

At the leading and trailing edges, x = ±c, Cp —> —oo. The latter result shows that the approx­imations involved in the linearization do not permit the method to be applied for local effects in the region of stagnation points, even when the slope of the thickness shape is finite.