Treatment of Shock Waves in Computational Methods

Shock waves have a definite structure with a thickness of only a few mean free paths. This would mean that for their computation the Boltzmann
equation must be employed [15]. In general the Boltzmann equation is valid in all four flow regimes, Section 2.3, i. e., from continuum to free molecular flow. In the free-molecular flow regime it is used as the so called collisionless Boltz­mann equation. However, due to the very large computational effort to solve it (recent developments in solution algorithms and computer power have im­proved the situation), discrete numerical continuum methods for the solution of the Euler and the Navier-Stokes/RANS equations and their derivatives will be employed in aerothermodynamics whenever possible. For computational cases, where a gap exists between the applicability range of the latter, and that of the Boltzmann equation, the bridging-function concept can be used [16].

The question is now how to solve the computational problem of shock waves in the continuum regime. In [17] it is shown that the structure of a normal shock wave can be computed with a continuum method, i. e., the Navier-Stokes/RANS equations, for pre-shock Mach numbers Mi ^ 2. This is done by comparing solutions of the Boltzmann equation, which employ the Bhatnagar-Gross-Krook model, with solutions of the Navier-Stokes equa­tions.

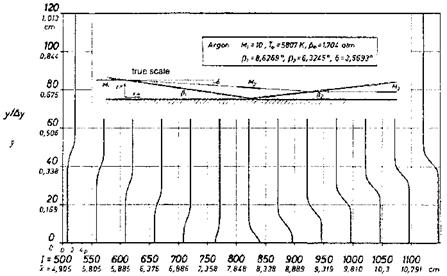
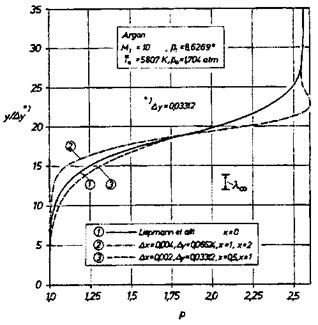
Since it is the Mach number MN normal to the front of the shock wave, which matters, also the structures of oblique shock waves can be treated with the Navier-Stokes equations, if MN ^ 2. We show this in Fig. 6.16 with the computation case of a reflecting shock wave at a surface without a boundary layer [18]. The case was set up such that the normal Mach number of the incoming shock wave, MN = M1 sin в = 1.5, was equal to that of a case treated in [17]. In Fig. 6.17 the solution of the Boltzmann equation (curve 1) [17] is compared at some station ahead of the reflection location, with solutions of a space-marching, shock-structure resolving scheme of a derivative of the Navier-Stokes equations [18].

For the coarse discretization of the latter solution with about ten nodes in the shock wave in stream-wise direction (curve 2) the comparison is not satisfactory. The fine discretization with about twenty nodes (curve 3) yields a good agreement on the high-pressure side (behind the shock wave). On the low-pressure side (ahead of the shock wave) the agreement is only fair. This could be due to the fact, that in [17] the Prandtl number Pr = 1 was used, and in [18] the actual value.

This brings us back to the original question of how to treat shock waves in flow fields past flight vehicles, which globally are fully in the continuum regime. Obviously a discretization with twenty nodes across the shock struc­ture is beyond the performance range of computers for a long time to come. Even if this would be possible, the problem remains, that shock-wave struc­tures can be described by means of the Navier-Stokes equations only if the relevant shock-wave Mach number is small enough.

In Euler and Navier-Stokes/RANS solutions shock waves therefore are treated as discontinuity surfaces in the frame of the “weak-solution con­cept”, see, e. g., [19]. This “shock-capturing” approach demands to employ the

governing equations in conservative formulation, Appendix A, see also Section 4.3. The “shock-fitting” approach, see, e. g., [20], which is applicable more or less only to describe the bow-shock surface of a vehicle, is now seldom used.

The shock-capturing approach is well proven. In the slip-flow regime, how­ever, where over a blunt body a “thick” shock wave can even merge with the also “thick” boundary layer (merged-layer regime [21]) the shock-capturing approach is somewhat questionable, also in view of the fact that the shock wave has a “secondary” structure due to thermochemical relaxation effects, Sub-Section 5.5.1.