Application of Vortex Theory

The relationships developed according to vortex theory for propellers in Chapter 4 can be used to predict the variation of CP with CT for a hovering rotor. The parameters that can be varied are the tip Mach number a>R/a0 = MT and the rotor geometry <jx and в. Needless to say, these

calculations are accomplished best on a digital computer. Because the vortex theory accounts for the continuous decrease of the rotor loading at the tips, it is possible with this theory to calculate, in detail, effects such as compressibility.

To use the preceding equations for a given rotor we assume a series of different collective pitch angles and calculate the CT and CP corresponding

to each в. The usual helicopter rotor employs a linear twist such that the blade pitch angle at any x is given by

в = 60 + 0Tx (5-6)

and a series of different в0 values is selected. The twist, 0T in Eq. (5-6), is usually negative and varies between 0 and approximately 15°.

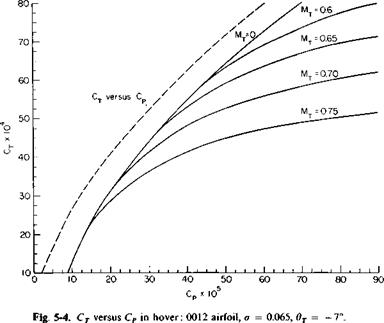
Calculated Results. A set of calculated curves of rotor thrust coefficients versus power coefficients is presented in Fig. 5-4. These curves are for a hovering rotor with a constant chord and total blade twist of 0T = —7°. The rotor solidity is 0.0651 and the section is an NACA 0012 airfoil section. The airfoil constants, already given for this airfoil were used for the calcula­tions. Also included in the figure is the variation of the induced power coefficient with the thrust coefficient. This curve was obtained by setting e equal to zero. The reader may verify for himself that for a given CT the value of CP., as read from the graph, is approximately 10 to 15% higher than

the value obtained from simple momentum theory according to Eq. (5-4). This is the result of tip losses calculated by the use of Prandtl’s tip loss factor F.

The severe effect on the required power caused by exceeding the critical Mach number at the tip of the rotor is clearly evident from Fig. 5-4. For example, at a tip Mach number of 0.7, the power required to sustain a given thrust rises rapidly above a CT of 36 x 10-4. For a tip Mach number of 0.6 the value of the power-divergent CT is increased to approximately 60 x 1СГ4.

The difference between the total CP curves and the CP. curve is that part of CP contributed by the profile drag of the blades. For this particular rotor it is seen that in the region of zero compressibility losses the profile power coefficient CP varies from 7 x 10"5 at low thrust coefficients to 9 x 10-5 at the higher CT values. This slight increase in the CPp is caused by the increased section lift coefficients at the higher thrust coefficients.

For a constant Cd and C, = 0 the profile power coefficient becomes

ado

8

For the rotor in Fig. 5-4 <50 = 0.0085 so that CP = 1 x 10“5, which agrees closely with the value read from the figure at low thrusts.

Similar calculations of CT versus CP, based on the application of Prandtl’s tip loss factor to vortex theory, confirmed remarkably well the test results reported in Ref. 5. These calculations were for other rotors with different twists and airfoil sections operating at high tip Mach numbers.

Figure 5-4 can be used to predict the performance of other hovering rotors, provided their geometry does not vary too much from the rotor on which Fig. 5-4 is based.

Corrections to CP versus CT for Minor Rotor Changes. The total CP can be written approximately as

CP = CPi + CPp ~ (5-8)

An average rotor CL, denoted by CL, can be calculated from Eq. (4-21) for X = 0 and in terms of the CT defined by Eq. (5-2) is

— 6 Ct

CL = – f, (5-9)

if CD is related to CL by

CD = 50 + kC.

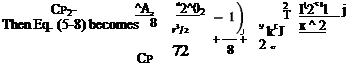Thus the difference in CP between two rotors, 1 and 2, compared at the same thrust coefficient, would be

°A2 _ j ,*A,

but cr^Oj/8 is the profile power coefficient for the number one rotor at zero thrust coefficient, CP, whereas (9/2’^Ckjal) is the difference between the profile power coefficient at the thrust under consideration and CPpl(0). Therefore:

By substitution of the more exact values of CPpl and CPpi(0|, as read from Fig. 5-4, the errors involved in the approximation of Eq. (5-8) are minimized.

As an example in the use of Fig. 5-4 and Eq. (5-10) suppose we wished to determine the power coefficient required for a thrust coefficient of CT = 5 x 10“3 for a rotor with a solidity of a = 0.05 and a 0012 airfoil section at a tip Mach number of 0.54. The reference rotor (No. 1) will, of course, be the one for which Fig. 5-4 is calculated. Thus, from Fig. 5-4,

al = 0.0651,

CPpl = 8 x 10“5 (g, CT = 5 x 10“3,

CPpim = 7 x 10-5 @ Cr = 0,

CPl = 36 X 10“5.

Because the airfoil section is unchanged, k2 = kt and d02 = <50l. There­fore

Cp2 — CPl + (CP2 CPl)

= 36 x 10“5 + 7 x 10“5(0.766 – 1) + 1 x 10“5(1.31 – 1)

= 34.67 x 10"5.

At this thrust coefficient the calculations indicate that some power would be saved by reducing the rotor solidity. Of course, this method of extra­polation does not account for possible differences in compressibility effects, which can be found only by exact calculations. However, an approximate check of the compressibility effects that might be expected can be obtained

from Fig. 5-4 (at least for the 0012 section) by calculating the average rotor CL at which power divergence occurs for a given Mach number. For this example it can be seen that for a tip Mach number of 0.54 the power – divergence CL is

For the new rotor of a = 0.05, CL at CT — 50 x 10-4 is equal to 0.6, which is below the power-divergence value for this Mach number, and thus differences in compressibility effects should be minor. For a change in the airfoil section values of <50г and k2 will have to be estimated from drag polars. Differences in compressibility effects can be estimated approximately by adjusting the values of the tip Mach numbers by the difference between the critical Mach number of the new section and that of the 0012 section.