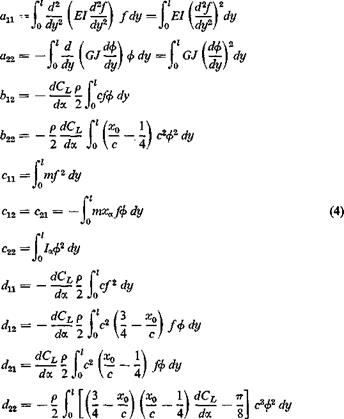APPROXIMATE DETERMINATION OF THE CRITICAL SPEED BY GALERKIN’S METHOD

We shall consider the motion at the critical flutter condition and determine the critical speed of flight. In the following, therefore, U represents the Ua of the preceding section. The motion is harmonic and representable as

h = Af(y)eM, а = Вф(у)еш (1)

where со is real and A, В are complex constants.

We assume A and В to be of the same dimensions as h and a, respec­tively, and f(y), ф(у) to be dimensionless. Substituting Eqs. 1 into the differential equation 3 of § 6.3, and canceling the factor e’“" throughout, we obtain

These are simultaneous differential equations with complex coefficients. The boundary conditions are given by Eqs. 4 of § 6.3, provided that the h and a functions were replaced by/and <f>.

As a first approrximation to the critical speed and frequency, the method of Galerkin may be used.118 Assume that the functions f(y) and <j>(y) are known and real valued. Multiplying the first of Eqs. 2 by f(y) dy and the second by ф(у) dy, and integrating from 0 to /, we obtain

A(an — cno)2 + ia>Udn) + B(c12u>2 — b12U2 — /со Ud12) — 0 A(c21oj2 — ia>Ud21) + B(a22 — c22a>2 b22U2 + imUd22) = 0

where*

The homogeneous equations 3 admit nonvanishing solutions A, В only if the determinant of their coefficients vanishes. This determinant being complex, both the real and imaginary parts must vanish. On setting the determinant to zero and separating the real and imaginary parts, we obtain two equations:

The sign in front of the radical must be chosen in such a way as to give the smallest positive value of U2.

Thus a solution can be obtained if the flutter modes / and ф are known. But they are not known at the beginning. Hence, it is necessary to approximate them on the basis of empirical information.[17] As a simple approach,/and ф may be assumed to be the fundamental modes of purely
flexural and purely torsional oscillations in still air, of a cantilever beam of uniform cross section:

J{y) — cosh ку — cos ку — 0.734 (sinh ку — sin ку) (11) where к = 1.875//, and

ф(у) = sin^ (12)

For these functions, tables for the integrals off2(y), ф2(у),/(у)ф(у), etc., are available.6-25

When the distances from the centers of mass to the elastic axis are large, or the wing planform is such that the oscillation modes differ considerably from those of a uniform beam, better results can be obtained by assuming f(y) and ф(у) as the coupled flexure-torsional oscillation modes of a wing. The predominantly torsional mode should usually be used. Sometimes it is advantageous to use the uncoupled flexure and torsion modes of the actual wing for/ and ф.

Corresponding to the two solutions of V2 from Eq. 10, there are two values of со2 from Eq. 7. Usually the smaller t/2 is associated with the higher со2; for, in Eq. 7, the coefficients Bx and Dx are always positive, whereas Z)2 is negative if the elastic axis lies behind the 1/4-chord point, as is usually so. Since, for conventional wings the torsional frequency (in still air) is higher than the flexural, the above conclusion indicates that the flutter mode is generally predominantly torsional.

It has been shown by a simple example in § 1.9 that the oscillations at different spanwise coordinates of a beam of variable cross section with damping are out of phase. Since at the critical flutter condition the aerodynamic force has a component proportional to dh/dt and Эа/Эt, (of the nature of a “damping” force), it is natural to expect that the flutter mode is also generally out of phase in the spanwise direction Mathe­matically, this means that the functions Дг/) and ф(у) must have complex coefficients (see § 1.9). This is actually true, but the change in phase angle along the span is generally small. By assuming f(y), ф(у) to be real func­tions, little error will result. On the other hand, the ratio AjB, solved from Eqs. 3, when the critical value of со and U are used, is generally com­plex, indicating a shift of phase between the flexural and torsional motion. This phase shift is of fundamental importance in governing the energy exchange between the wing and the flow, as we have shown in § 5.4.