Boundary Layer Response to Pressure and Shear Gradients
If we temporarily redefine s, n to be parallel and normal to some particular streamline, then locally v = 0 in these coordinates, and the s-momentum equation becomes
which provides an estimate of the change in a fluid element’s velocity Au over some small distance As.
du peue 1 дт
All, ~ — as = ————————- Aue + —— as (4.24)
ds pu pu dn
 |
 |
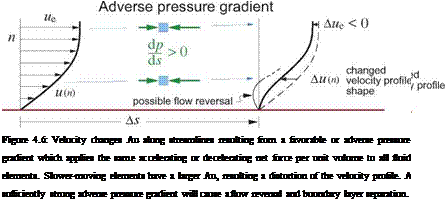
The first term on the right in (4.24) represents the effect of a streamwise pressure gradient dp/ds. Of particular importance is the factor peue/pu which “magnifies" any edge velocity change Aue into a larger change Au inside the boundary layer, as shown in Figure 4.6.
When dp/ds < 0 we have a favorable pressure gradient. This corresponds to due/ds > 0, so this is also called an accelerating boundary layer. As pictured at the top of Figure 4.6, the pressure gradient applies the same accelerating force per unit volume to all the fluid elements in the boundary layer, but the slower element responds more strongly due to its larger peue/pu factor in (4.24).
When dp/ds > 0 we have an adverse pressure gradient. This corresponds to due/ds < 0, so this is also called a decelerating boundary layer, pictured at the bottom of Figure 4.6. In this case we have the possibility of flow reversal near the wall, which results in flow separation where the bulk of the shear layer lifts off the wall as shown in Figure 4.4 on the right. This also results in rapid increases in the mass defect, and thus produces strong viscous displacement effects on the outer potential flow.
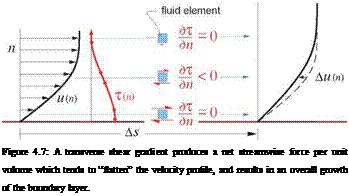
Unlike the streamwise pressure gradient which is uniform across the boundary layer thickness, the transverse shear gradient дт/dn varies strongly across the layer and applies different streamwise forces to different fluid elements, as shown in Figure 4.7. These variations in the shear forces persistently tend to “flatten” the velocity profile, and their cumulative effect is to cause the overall boundary layer to thicken downstream. The shear gradient also provides a negative feedback in the streamwise momentum equation, in that it acts to partially counter the possibly rapid u(n) profile shape distortions caused by streamwise pressure gradients.
 —— Tin)
—— Tin)











