CLASSICAL SOLUTION OF THE LIFTING PROBLEM
The solution for the velocity distribution, pressure difference, and the aerodynamic loads on the thin, lifting airfoil requires the knowledge of the vortex distribution y{x) on the airfoil. This can be obtained by solving the integral equation (Eq. ((5.39)), which is a form of the zero normal flow boundary condition. The classical approach (e. g., Glauert,52 p. 88) is to approximate y(x) by a trigonometric expansion and then the problem reduces to evaluating the values of this expansion’s coefficients. Therefore, a transformation into trigonometric variables is needed. Such a transformation is described by Fig. 5.9 and is
jc =^(1 – cos в) (5.45)
and
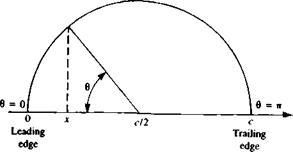 |
dx = I sin в dd (5.45a)
Note that the airfoil leading edge is at x = 0 (0 = 0), and the trailing edge is at x = с (0 = я). Substituting Eq. (5.45) into Eq. (5.39) results in the transformed integral equation.
0< в< я
This integration with 0O should hold for each point x (or 0) on the airfoil. The transformed Kutta condition now has the form
у(л) – 0 (5.47)
The next step is to find a vortex distribution that will satisfy these last two equations. A trigonometric expansion of the form
X A„ sin (я0)
n = l
will satisfy the Kutta condition, and is general enough that it can be used to represent the circulation distribution. However, experimental evidence shows a large suction peak at the airfoil’s leading edge, which can be modeled by a function whose value is large at the leading edge and reduces to 0 at the trailing edge. Such a trigonometric expression is the cotangent function, which will be included, too, in the proposed vortex distribution:
The suggested solution for the circulation is shown graphically in Fig. 5.10, and in order to cancel the 2term on the right-hand side of Eq. (5.46) the proposed function for the vortex distribution will be multiplied by this constant:
У(0) = 2(2®[а0—+ 2) A„sin(n0)l (5.48)
L sin 0 я=і J
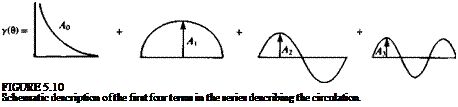 |
An additional advantage of the first term is that it induces a constant downwash on the airfoil, as will be evident later on (see Eq. (5.53)). In order to determine the values of the An constants, Eq. (5.48) is substituted into Eq.
(5.49)
In this equation, each point 0 is influenced by all the vortex elements of the airfoil—this requires the evaluation of the integral for each value of 0. Recalling Glauert’s integral
![]() fя COS П0О,7rsinn0
fя COS П0О,7rsinn0
— s——- —2de0 = ——
and replacing 1 by cos 00, the first term of the integral becomes
1 . Г cos O0o + cos 0O sin 0O de0 1 . . .
—— r—z———- 2——- о=“~Ло(0 + л:) = – A0
Л J0 sin 0O cos 0O – COS 0 Л
whereas for the terms with the coefficients A,,A2,…, the following trigonometric relation is used:
sin /100 sin 0O = ^ [cos (n — 1)0O — cos (n + 1)0O] n = 1, 2, 3,…
This allows the presentation of the nth term in the following form:
1 г Г„ • / л i sin 00 de0
— I A„ sin (n0o) ——————-
Я Jo 1 П cos 0O – cos 0
__ А гЛ ACL
![]() = ——- [cos (n – 1)0O – cos (n + 1)0O] 0
= ——- [cos (n – 1)0O – cos (n + 1)0O] 0
2n Jo
and by using Glauert’s integral this reduces to
An fsin(n-l)0 sin (n + 1)01 2л L sin 0 sin 0 J
![]()
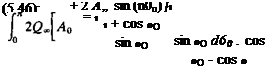 |
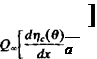 |
j = An cos (n0)
Substituting this into Eq. (5.49) yields
-A0 + 2 An cos (n&) = ~~T~~ ~ a (5.50)
«=i dx
This is actually a Fourier expansion of the right-hand side of the equation, which includes the information on the airfoil geometry. Multiplying both sides of the equation by cos тв and performing an integration from 0-* я, for each value of n, will result in the cancelation of all the nonorthogonal multipliers (where тФп). Consequently for each value of n the value of the correspond-
ing coefficient A„ is obtained:
2 [ йПс(в)со&пвав n = 1, 2, 3, . . . (5.52)
л Jo dx v ‘
Note that Eq. (5.50) can be rewritten as an expansion of the downwash distribution w = w(d) on the airfoil as
jr = – Ao + E An cos (пв) (5.53)
n = l
and it is clear that the downwash due to the first term (multiplied by A0) of the vortex distribution is constant along the airfoil chord.
The slope drjc/dx can be expanded as a Fourier series such that
and a comparison with Eq. (5.50) indicates that B0=a-A0 Bn=An n =
This allows the simplification of Eq. (5.53) such that the angle of attack and camber contributions to the downwash are explicitly displayed. A replacement of the An coefficients with the B„ coefficients in Eq. (5.53) results in
= – a + 2) B„ cos (пв) (5.53a)
Q°° n=0













