Effect of Mean Flow Variation on the Scattering

In a swirling mean fbw various radial profiles can be obtained by consid­ering different combinations of free vortex and rigid body swirl. To illustrate how the radial variation of the mean ft>w changes the aeroacoustic response, we consider four different mean ft>ws with the same total Mach number of 0.4062 at the mean radius. The first mean ft>w is axial and uniform. The three swirling ft>ws have the same axial and swirl Mach numbers of 0.3536 and 0.2, respectively, at the mean radius and consist of a free vortex swirl distribution with Mr = 0.2, a rigid body swirl with Mq = 0.2 and a combination of free vortex and rigid body swirl, Mr = 0.1 and Mq = 0.1. The c/rm ratio at the mean radius is 0.3491, Co = 3n, mg = B = 16, V = 24, rh/rt = 0.6 and a grid of {nx x щ x nr} = {161 x 21 x 21} is used. The gust radial component Ur = 0, and its upwash a(u) = 1. For the uniform ft>w, only one propagating acoustic mode (-8, 0) exists, while two propagating modes [(-8,0), (-8,1)] exist for the three swirling flows.

Figure (3) compares the absolute value of the unsteady lift coefficient along the span for the different mean flows. The figure shows significant difference in the value and variation trend between the uniform flow case and the swirling flow cases indicating that the swirl effect significantly modifies the unsteady lift. The differences in the lift coefficient of the three swirling ft>ws are not significant. We now examine the magnitude of the upstream and downstream acoustic coefficients presented in Table (1). The table shows that the down­stream acoustic coefficients are larger than those upstream for all mean flows. However, the difference between the downstream and upstream acoustics is much larger in the swirling flows than in the uniform flow.

Although the swirl radial distribution (blade twist) does not seem to have much effect on the magnitude of the unsteady lift coefficient, it has a signif­icant effect on both upstream and downstream acoustic coefficients as shown in Table (1). The acoustic energy scattered by the incident gust is larger for the rigid body swirl distribution than that of the combined swirl which is larger than that of the free vortex. We also note that for the free vortex case most of the energy is scattered in the first mode whereas the second mode dominates for the rigid body swirl. In order to explain this result, we examine the incident gust radial phase variation. Since the gust is nearly convected and the distance travelled from the inlet to the leading edge in our computational domain is about a chord length c << rm, the quantity a defined by equation(7) gives a good estimate of the gust phase. For a rigid body swirl, a increases by n/2 from hub to tip, whereas for the free vortex it increases by 3.28n. This affects the sectional lift phase but not its magnitude. However, the scattered acoustic energy which depends on the entire radial distribution of the gust is strongly affected.

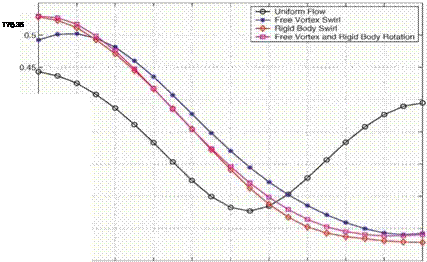Figure 3. Comparison of the magnitude of the lift coefficient for different mean Ibws. rh / rt =0.6 and d = 3n