Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Flying with minimum drag
Now, on first thoughts, we might think that flying with minimum drag meant presenting the aeroplane to the air in such an attitude that it would be most streamlined; in other words, in the attitude that would give least drag if a model of the aircraft were tested in a wind tunnel. But if we think again, we shall soon realise that such an idea is erroneous. This ‘streamlined attitude’ would mean high speed, and the high speed would more than make up for the effects of presenting the aeroplane to the air at a good attitude; in a sense, of course, it is the streamlined attitude that enables us to get the high speed and the high speed, in turn, causes drag. We are spending too much effort in trying to go fast.
On the other hand, we must not imagine, as we well might, that we will be flying with least drag if we fly at the minimum speed of level flight. This would mean a large angle of attack, 15° or more, and the induced drag particularly would be very high – we would be spending too much effort in keeping up in the air.
There must be some compromise between these two extremes – it would not be an aeroplane if there was not a compromise in it somewhere. Perhaps, too, it would not be an aeroplane if the solution were not rather obvious – once it has been pointed out to us! Since the lift must always equal the weight, which we have assumed to be constant at 50 kN, the drag will be least when the lift/drag ratio is greatest. Now, the curve of lift/drag ratio given in Fig. 3.16 refers to the aerofoil only. The values of this ratio will be less when applied to the whole aeroplane, since the lift will be little, if any greater, than that of the wing alone, whereas the drag will be considerably more, perhaps twice as much. Furthermore, the change of the ratio at different angles of attack, in other words, the shape of the curve, will not be quite the same for the whole aeroplane. None the less, there will be a maximum value of, say 12 to 1 at about the same angle of attack that gave the best value for the wing, i. e. at 3° or 4°, and the curve will fall off on each side of the maximum, so that the lift/drag ratio will be less, i. e. the drag will be greater, whether we fly at a smaller or a greater angle of attack than 4°; in other words, at a greater or less speed than that corresponding to 4°, which our table showed to be 160 knots.
A typical lift/drag curve for a complete aeroplane is shown later on in Fig. 6.3, and Table 5.2 shows the sort of figures we shall get from it,
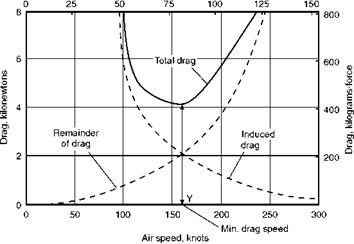
This table is very instructive, and shows quite clearly the effect of different air speeds in level flight on the total drag that will be experienced. It shows, too, that the least total drag is at the best lift/drag ratio, which in this case is at 4° angle of attack, which, in turn, is at about 160 knots air speed (Fig. 5.10, overleaf).
The angle of attack that gives the best lift/drag ratio will be the same whatever the height and whatever the weight; it is simply a question of presenting the aeroplane to the air at the best attitude, and has nothing to do with the
|
Table 5.2 Airspeed and drag
|
density of the air, or the loads that are carried inside the aeroplane, or even the method of propulsion.
This means that the indicated air speed, which is what the pilot must go by, will be the same, whatever the height, but will increase slightly for increased loads. The same indicated air speed means the same drag at any height, and therefore the same range.
On the other hand, the higher speed which must be used for increased weights means greater drag, because, looking at it very simply, even the same lift/drag ratio means a greater drag if the lift is greater. So added weight means added drag – in proportion – and therefore less range – also in proportion.
Tet us go back to the newton metres, the 7 600 000 joules that we hope to get from 1 litre of fuel. How far can we fly on this? At 100 knots we shall be able to go 7600 000 divided by 8330, i. e. about 912 metres; at 120 knots 1610 m; at 140 knots 1792 m; at 160 knots 1822 m; at 180 knots 1627 m; at 200 knots 1292 m; and at 220, 240, 260 and 280 knots, 1095, 912, 790, 684 metres respectively, and at 300 knots only 577 metres. These will apply at whatever height we fly. If the load is 60 kN instead of 50 kN each distance must be divided by 60/50, i. e. by 1.20; if the load is less than 50 kN each distance will be correspondingly greater.
Now to sum up this interesting argument: in order to obtain the maximum range, we must fly at a given angle of attack, i. e. at a given indicated air speed, we may fly at any height, and we should carry the minimum load; but if we must carry extra load, we must increase the air speed.
That is the whole thing in a nutshell from the aeroplane’s point of view. Unfortunately, there are considerations of engine and propeller efficiency, and of wind, which may make it advisable to depart to some extent from these simple rules, and there are essential differences between jet and propeller propulsion in these respects. We cannot enter into these problems in detail, but a brief survey of the practical effects is given in the next paragraphs.
|
Air speed, metres per second
|
Fig 5.10 Flying for maximum range: how the total drag is made up Induced drag decreases with square of speed. Remainder of drag increases with square of speed. Total drag is the sum of the two; and is a minimum when they are equal.
Another way of thinking of the significance of flying with minimum drag is to divide the total drag into induced drag – which decreases in proportion to the square of the speed – and all-the-remainder of the drag – which increases in proportion to the square of the speed. This idea is well illustrated in Fig. 5.10 and in the numerical examples (Appendix 3).
