INFLUENCE OF ASPECT RATIO AND FORM

As pointed out before, the derivatives of control-flap forces and moments can be taken in such a manner that they are theoretically independent of the aspect ratio of wing or tail surface. Actually, a flow pattern similar to two-dimensional cannot be expected to exist at and near the lateral edges. Other deviations must be expected on account of plan-form shapes different from rec­tangular and straight, such as sweepback in particular.

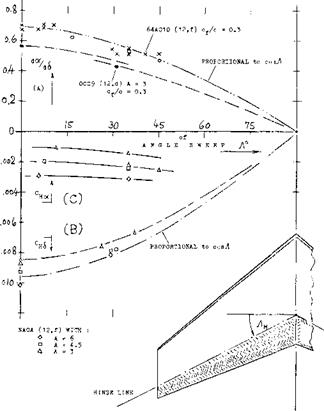
INFLUENCE OF ASPECT RATIO. Lifting surfaces have tips, ends or lateral edges where the pressure distribution is no longer similar to two-dimensional. The influence of finite span upon the control character­istics is conveniently considered in terms of the aspect ratio. A systematic investigation into forces and moments of plain horizontal tail surfaces as a function of the A’ratio is specifically reported in (4,c, d). Figure 10 presents the influence in terms of the derivatives explained in the first part of this chapter. Results for chord ratios be­tween 0.2 and 0.4 are as follows:

(a) 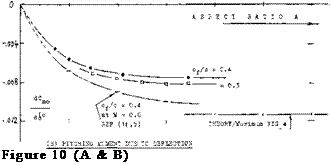The effectiveness ratio d<x/db hardly varies, down to A = 2. While a number of experimental values reported in (4,d, c) but not reproduced in figure 10-A,

indicates a decrease of the effectiveness ratio below A = 2 or = 1, lifting-surface theory (2,f) predicts an increase to unity, as the A’ratio approaches zero.

(b) 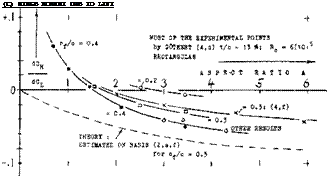The pitching moment dC^d^ reduces as the A’ratio is reduced. The change is similar to that of dCm./dCL (due to the linear lift component) as explained in the chapter on “straight wings”.

(c) The derivative dCq/dC^ reduces as the A’ratio is reduced; and it changes direction or sign, roughly between А з» 3 and = 1. The influence is still noticeable at least up to A = 5.

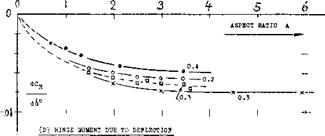
(d) The hinge moment due to flap deflection (at = constant) reduces in a manner similar to the pitch­ing moment under (b). Values which can, for practi­cal purposes, be accepted as constant, may be expected above A ^ 3.

(e) The deflection of a stick-free elevator or rudder (at zero hinge moment) not only reduces as the A’ratio is reduced, it can also change sign (at A between 2.5 and 1.5 as in the graph). The variation corresponds to that under (c).

(f) The increment of doC/dC^ due to stick-free con­trol flap, corresponds to the variation of the de­flection angle under (e). At and below A =. 2.5 or 1.5, the flaps of the tested configurations tend to move against the oncoming flow.

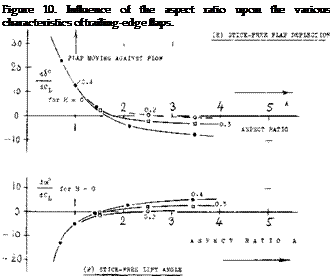INDUCED ANGLE. As explained in the chapter on “small aspect ratios”, the mechanism of circulation reaches a certain limiting condition, roughly at an as­pect ratio equal to unity. Below A — 1, and disregarding any “cross-flow” lift component (as at higher angles of attack), lift is produced “near” the leading edge, while the trailing edge contributes “nothing”, because of “complete” downwash. Lift and pitching moment pro­duced by,* and hinge moments of control flaps can thus be expected to decrease as the A’ratio is reduced. The variations as in parts (B) and (D) of figure 10 are thus explained. It must be noted, however, that in small aspect ratios, both the control surface as such, as the flap (when deflected) produce an additional non-linear lift component.

REVERSAL OF HINGE MOMENTS. Finite aspect – ratio (lifting-surface) theory in (2,f) confirms the reason­ing in the preceding paragraph. Evaluated in the form as in this text, the theory yields a hinge-moment derivative due to lift, reducing toward nothing, as the A’ratio ap­proaches zero. Part of the trend as in part (C) of figure 10, is thus explained. However, experimental results, if not below A — 2.5, then below A = 1.5, clearly de­monstrate a reversal of the moment, corresponding to a positive sign. This reversal is similar to that as found later (see figure 14) resulting from larger trailing-edge angles. It appears that the trailing-wedge effect is en­larged by the type of flow pattern past the afterbody of small-aspect-ratio wings.

SWEEPBACK. As a function of the angle of sweep, the lift curve slope (dC^/doc) of a series of wings having one and the same finite aspect ratio, reduces approxi­mately or not quite, in proportion to the cosine of the angle of sweep “Л ”; see the “swept wing” chapter. The angle of sweepback in tapered wings or control surfaces, measured in each half span at the flap hinge line, is somewhat smaller than the angle of sweep conventional­ly defined for. the quarter-chord line. It seems that the hinge-line sweep is applicable to the forces and moments of and due to flap deflection. We have, therefore, used this type of angle when plotting the experimental points in figure 11, wherever “<$ ” is involved. The deflection angle of a control flap (such as an elevator) measured in the direction of flow or flight, is only (cosA) times the angle 6 measured about the hinge axis. Tentatively, therefore, the lift-curve slope due to deflection (at con­stant angle of attack) may vary as

dCL /сіЛ ~ cos(30)

This variation is reasonably well confirmed in (12,f). As a consequence, the flap effectiveness ratio can be expected to vary as

dot/db ~ cosj (31)

Confirmation by experiments as in part (A) of figure 11, is acceptable. It is suggested, however, that the flow pat­tern is too much 3-dimensional for the lifting-line ap­proximation above.

Figure 11. Flap characteristics as a function of the angle of sweep of wing or control surface.

HINGE MOMENTS (of plain flaps) may be expected to be proportional to the lift produced by their de­flection. Therefore: dH/d6 ~ cos2A * Considering, however, the moment arm of any swept flap normal to its hinge axis, to reduce in proportion to cos. A, we obtain

C|_|£ ~ cos. A (32)

Confirmation is found in part (B) of figure 11. As far as the hinge moment due to lift or angle of attack is con­cerned, theory (12,g) predicts a modest increase as a function of sweepback. The results plotted in part (C) of the graph, confirm this prediction. The derivative, which is small in the first place, might also be considered to be independent of the angle of sweep.

PLAN-FORM SHAPE. It is explained in the chapter dealing with “straight wings”, that the lateral edges and the rear plan-form corners of a wing are important in regard to lift, and lift-curve slope. Examination of ex­perimental results shows that edges and corners also have an effect on forces and moments of and due to flaps. In particular:

The derivatives dC^/d6 and do(/d^ of a control surface having an elliptical plan form, are notice­ably reduced as against those obtained for a com­parable rectangular surface.

The magnitude of hinge-moment derivatives is re­duced; particularly dC^/dC^, thus providing in­creased (dC|_/do<) in stick-free condition.