Integral Boundary Layer Relations

4.5.1 Integral momentum equation

The integral momentum analysis begins by combining the continuity and s-momentum equations as follows.

^ і x*dP tw To ds

Integrating JQne[ equation (4.25)] dn term by term then gives the dimensional form of the von Karman integral momentum equation,

where we see the reappearance of the mass defect m = peue5* and momentum defect P = peu)0 which previously appeared in Section 4.2.2 in the mass and momentum flow comparisons between viscous and inviscid flows.

Dividing equation (4.26) by peu2 produces the exactly equivalent dimensionless form,

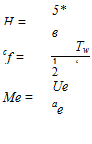
where the following new dimensionless parameters have been defined.

shape parameter skin friction coefficient

edge Mach number

The edge Mach number appears in (4.28) via the isentropic relation (1.78) between density and velocity differentials, which is valid for the edge quantities since these are in the inviscid flow.

dpe

Pe

The dimensional von Karman equation (4.26) is seen to govern the evolution of the momentum defect P, while the dimensionless form (4.28) governs the evolution of the related momentum thickness 0. The solution of (4.28) to determine 0(s) will be addressed in later sections.

4.5.2 Integral kinetic energy equation

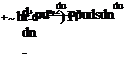An equation for the kinetic energy is obtained by multiplying the momentum equation by the velocity u. The mass equation is also incorporated to put the result into divergence form as follows.

— = V + ue6**

ds e ds where the kinetic energy defect К = 0* appealed previously in Section 4.2.2 in the kinetic energy flow comparisons between viscous and inviscid flows. New quantities which appear here are

Integrating J0”e [ equation

the density flux thickness which measures the work done (positive or negative) by the pressure gradient in conjunction with density variations across the boundary layer, and D is the dissipation integral which measures the local rate of flow kinetic energy dissipation into heat by the shear stress т acting on the fluid which is deforming at the shear strain rate du/dn. Note that 5** = 0 in incompressible flow where p/pe = 1, while D is always present and is virtually always positive (pt < 0 is very unlikely).

dfl* ds

2 H ** II*

9* due ue ds

Dividing equation (4.31) by ^peuI produces its exactly equivalent dimensionless form,

where the following new dimensionless parameters have been defined.

H * =	9* ~9	kinetic energy shape parameter
H**	5** ~f	density flux shape parameter
CD =	V Petl’e	dissipation coefficient

The dimensional kinetic energy equation (4.31) is seen to govern the evolution of the kinetic energy defect K, while the dimensionless form (4.35) governs the evolution of the related kinetic energy thickness 9*. The dimensionless kinetic energy equation (4.35) is used in some advanced integral calculation methods. See Rosenhead [11], Schlichting [12], and Drela et al. [6] for examples.