Laws of vortex motion
The theoretical modelling of the flow around wings was discussed in the previous section. There the use of an equivalent vortex system to model the lifting effects of a wing was described. In order to use this theoretical model to obtain quantitative predictions of the aerodynamic characteristics of a wing it is necessary first to study the laws of vortex motion. These laws also act as a guide for understanding how modern computationally based wing theories may be developed.
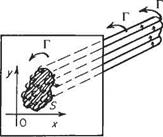
In the analysis of the point vortex (Chapter 3) it was considered to be a string of rotating particles surrounded by fluid at large moving irrotationally under the influence of the rotating particles. Further, the flow investigation was confined to a plane section normal to the length or axis of the vortex. A more general definition is that a vortex is a flow system in which a finite area in a normal section plane contains vorticity. Figure 5.5 shows the section area S of a vortex so called because S possesses vorticity. The axis of the vortex (or of the vorticity, or spin) is clearly always normal
|
|
Fig. 5.5 The vorticity of a section of vortex tube
to the two-dimensional flow plane considered previously and the influence of the so-called line vortex is the influence, in a section plane, of an infinitely long, straight-line vortex of vanishingly small area.
In general, the vortex axis will be a curve in space and area S will have finite size. It is convenient to assume that S is made up of several elemental areas or, alternatively, that the vortex consists of a bundle of elemental vortex lines or filaments. Such a bundle is often called a vortex tube (c. f. a stream tube which is a bundle of streamlines), being a tube bounded by vortex filaments.
Since the vortex axis is a curve winding about within the fluid, capable of flexure and motion as a whole, the estimation of its influence on the fluid at large is somewhat complex and beyond the present intentions. All the vortices of significance to the present theory are fixed relative to some axes in the system or free to move in a very controlled fashion and can be assumed to be linear. Nonetheless, the vortices will not all be of infinite length and therefore some three-dimensional or end influence must be accounted for.
Vortices conform to certain laws of motion. A rigorous treatment of these is precluded from a text of this standard but may be acquired with additional study of the basic references.[23]