LINEARIZED THEORY OF SMALL – DISTURBANCE COMPRESSIBLE FLOW

The potential flow model was based so far on the assumption of an incompressible fluid. In the case when the disturbance to the flow is small, it is possible to extend the methods of incompressible potential flow to cover cases with small effects of compressibility (e. g., low-speed subsonic flows). To investigate this possibility, the continuity equation (Eq. (1.21)) is rewritten in the form:

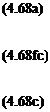— 1 (dp dp dp dp du dv dw ^^ + Ulb + Vty + Wlte)~lb+ty + lk

and the inviscid momentum equations (Eqs. (1.31)) are

du du du du —1 dp

—- 1- и ——- v 1- w —=— —-

dt dx dy dz p dx

dv dv dv dv —1 dp

dt dx dy dz p dy

dw dw dw dw — 1 dp

_ + м__ + и__ + и,_ = — — dt dx dy dz p dz

For an isentropic fluid the propagation speed of the disturbance a (speed of sound) can be defined as

,2 З?

dp

and consequently the pressure terms in the momentum equation can be replaced (e. g.,

3P 2^P

dx dx’

in the x direction). Now multiplying the momentum equations by u, v, and w,

respectively, and adding them together leads to

du dv dw 0du 0dv, dw du dv

u — + v— h w —- + U— + V—+W — + uv — + uv —

dt dt dt dx dy dz dy dx

—a[1] ( dp dp dp ~Vu’di + v~dy + w~dd

du dw dv dw

+ uw — + uw —— + vw h vw —

dz dx dz dy

Jl) du _ VW dv 2-у-— 2-у—- a2 dy a2 dz

Replacing the right-hand side with the continuity equation and recalling the irrotationality condition (Eq. (2.12), V X q = 0), results in

Using the velocity potential Ф as defined in Eq. (2.19), and assuming that the free-stream velocity Q„ is parallel to the x axis (thus Q„ becomes {/„), and that the velocity perturbations caused by the motion of the body in the fluid are small, we get

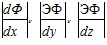(4.71)

Based on these assumptions, the velocity components, in terms of the perturbation velocity potential, are

и = LL +

ЭФ

dz

Assume steady state flow (d/dt = 0), and neglecting the smaller terms in Eq. (4.70), based on Eq. (4.71), this results in

/ n2 du dv dw

a2) dx + dy + dz

„ Э2Ф д? Ф Э2Ф (1-МІ)—Ї + —Ї + —Ї = 0

dy2 dz2

By using the energy equation for an adiabatic flow, it can be shown that the local speed of sound can be replaced by its free-stream value and the small-disturbance equation becomes

For time-dependent flows the dp/dt term in Eq. (4.70) needs to be evaluated

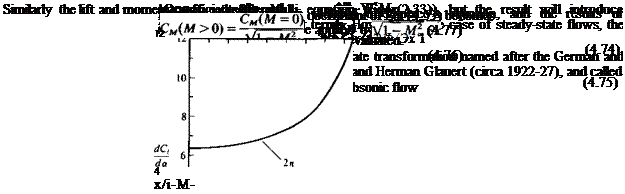which indicates that at higher speeds the lift slope is increasing as shown by Fig. 4.14. Also, note that according to Eq. (4.74) the x coordinate is being stretched as the Mach number increases and therefore the results for M = 0 and M > 0 are for wings of different aspect ratio.

Based on the results of Fig. 4.14 (for a two-dimensional airfoil), for small-disturbance flows the potential flow based models of this chapter are applicable at least up to = 0.6.