Noise Control by Vane Lean

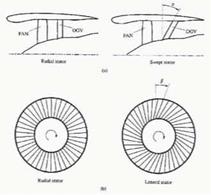
Lean is defined as the azimuthal displacement, в, of the vane leading edge from its baseline radial position, as shown in Figure 2. The positive lean angle, is in the counter clockwise direction. With this definition, positive lean corre­sponds to the direction of propagation of the upstream disturbances considered

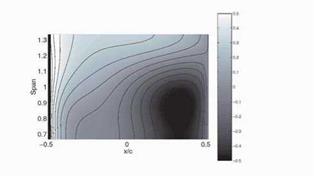
Figure 2. Real component of unsteady pressure difference across vane span for zero lean and sweep, C = 3n, Mx = 0.5

in the present work. Spanwise phase variation of the disturbance up-wash will depend on the lean angle. This phase variation is responsible for the noise re­duction or amplification. Classically, for a single airfoil, an incident gust with spanwise phase variations reduces the unsteady blade loading and propagating sound (Atassi, 1994). Thus we may argue that increasing vane lean, which increases the incident disturbance spanwise phase variation, will also reduce the perceived noise levels. However, this is not the case. Schulten, 1982, has demonstrated that vane lean increases the noise level, and the quietest configu­ration was for zero vane lean. On the other hand, Envia and Nallasamy, 1999, have concluded that lean is always effective in the negative direction. In this section we examine the results found in the previous studies, and attempt to resolve the differing conclusions.

We consider two test geometries, and an incident disturbance with a reduced frequency Cj = 3n. For the first geometry, B = 23, V = 24, and there are three propagating acoustic modes (c-1,0,c-1,1,c-1,2). This case is similar to that studied by Schulten, 1982. For the second geometry, B = 16, V = 24, which is a more relevant case for a real engine configuration. For that case there are two propagating modes (c_8,o, c_8,i). Both studies are carried out to (i) compare and validate results with those of Schulten and (ii) examine the effectiveness of vane lean for realistic fans.

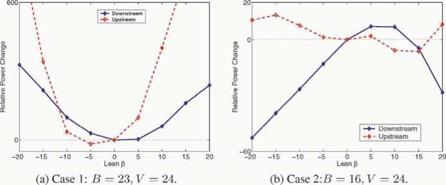
Validation Case: B = 23, V = 24. For this test case the number of rotor blades and stator vanes are chosen such that the propagating modes have an azimuthal mode number m = — 1. Figure 3 a shows the RAPC versus the lean angle. It is clear that lean is totally ineffective for this rotor/stator configura­tion with a significant power increase for any lean angle. These results are in agreement with calculations performed by Schulten for a similar geometry.

Figure 3. Relative power change for downstream and upstream sound power levels for dif­ferent lean angles. Solid lines represent downstream, and dashed lines upstream sound power change

Benchmark Case: B = 16, V = 24. For the benchmark test case the

number of rotor blades and stator vanes are chosen such that the propagating modes have an azimuthal mode number m = —8. Figure 3b shows the RAPC versus the lean angle. The downstream sound power is significantly reduced for negative and for large positive lean angles. Lean is not effective for the upstream sound power, as also found by the previous investigators. This is attributed to the smaller wavelength of the upstream propagating waves.

Analysis of Lean Effectiveness. Figure 3 indicates that vane lean can be effective or ineffective depending on the rotor/stator geometry. This seems to counter classical results mentioned earlier, than an oblique gust increases the unsteady spanwise pressure distribution, reducing the unsteady lift and prop­agating sound power (Atassi, 1994). In order to understand and explain the results of Figure 3, we examine the modal composition of the propagating modes.

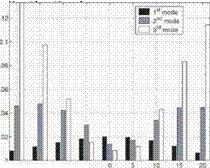
Lean generates a spanwise phase variation of the disturbance up-wash on the vane surface. For uniform fbw this phase variation is proportional to e img e. The larger the lean angle, в, the stronger the phase variation. As shown in Elhadidi, 2002, Atassi et al., 200x, radial gust variations excite and couple with higher order propagating modes. Because of the spanwise phase variation caused by vane lean, the amplitude of the first propagating mode will reduce, whereas, the amplitude of the higher order modes may increase. As a result, for lean to be effective the power reduction contributed from the first mode must be larger than the power increase contributed from the higher order modes. Figure 4 compares the real component of the propagating pressure eigenmodes, ^ (cmn Pmn), for the zero lean case, and Figure 5 compares the amplitudes of the downstream acoustic modes, |cmn |, for various lean angles.

Figure 4. Spanwise variation of the real part of the unsteady pressure of the acoustic propa­gating modes for the two test cases at zero lean C = 3n, Mx =0.5

For the validation test case, the first propagating acoustic mode is almost a plane wave, and the amplitude of the downstream acoustic pressure decreases as lean is varied from its zero position as seen in Figure 5a. However, the second and third modes amplify at a faster rate than the reduction of the first mode. This accounts for the relative power increase with lean and explains the conclusions of Schulten, that lean is ineffective.

For the second test case, the amplitude of the first mode is reducing for all lean angles, as seen in Figure 5b. For negative lean angles there is an initial increase in the amplitude of the second mode, then a reduction. The increase in the second mode at negative lean angles is smaller than the reduction of the first mode thus reducing the overall sound power. Similarly as the amplitude of the second mode decreases for large positive lean angles, positive lean becomes efficient in the overall sound power reduction.

(b) Case 2: В = 16, V = 24.

Figure 5. Comparison of downstream acoustic pressure intensity for a reduced frequency C = 3n, Mx =0.5 for different lean angles

Schulten suggested that the azimuthal mode number m of the propagating modes is not likely responsible for the increase in the sound power as shown in Figure 3. Rather he attributed this rise to the radial force component acting on the vanes as a result of the lean. We note that Schulten built his conclusions on a single case where m = -1. Our results for m = -8, show a significant reduction in the acoustic power, thus indicating the importance of the modal composition and the coupling of the cascade response with the gust radial vari­ations.

Lean Effectiveness at Different Reduced Frequencies. The reduced fre­quency mainly affects the number of propagating modes in the duct. As a result lean effectiveness strongly depends on the reduced frequency. Figure 6 compares the RAPC for different lean angles at different reduced frequen­cies, for the geometry proposed by Hanson, 1999. For the first two frequencies Cj = 2n, 2.5n there is one propagating mode, the sound power is significantly reduced for negative lean. For the third and fourth cases there are two prop­agating modes and the effectiveness of lean is reduced. This is due to the relative increase in amplitude of the second mode over the reduction of the first mode. For the last two test frequencies C = 4n, 4.5n there are four prop­agating modes (c_8,o, c_8,i, c_8,2, ci6,o) and lean becomes even less effective. For C = 4n, the reduction of the first mode no longer overcomes the increase of the higher order modes.