Other Anti-Torque Devices

Besides the conventional tail rotor, other types of anti-torque devices are used on modem helicopters. These are the fenestron (or fan-in-fin or fantail) and the NOTAR concepts. All have relative advantages and disadvantages compared to a conventional tail rotor.

6.10.1 Fan-in-Fin

Shrouded or ducted fan anti-torque designs, which are known as “fenestrons,” “fan- in-fin,” or “fantail” designs, have been frequently considered over conventional tail rotors, especially for smaller and lighter helicopters. A photograph and schematic of a fan-in-fin design is shown in Fig. 6.35. Details of the design of such anti-torque devices are given by Mouille (1970, 1979), Mouille & Dambra (1986), Vuilet & Morelli (1986), Vialle & Amaud (1993), and Abrego & Bulaga (2002). Fan-in-fin designs typically are found to have lower power requirements than an open tail rotor to produce the same amount of thrust. Alternatively, this means the fan-in-fin design can give the same anti-torque and yaw authority with a smaller and perhaps lighter design compared to a conventional tail rotor. See also Davidson et al. (1972) for the design trades.

Vertical fin

Figure 6.35 The fan-in-fin or fenestron tail rotor, as used on the SA-365 Dauphin.

w = vJa,

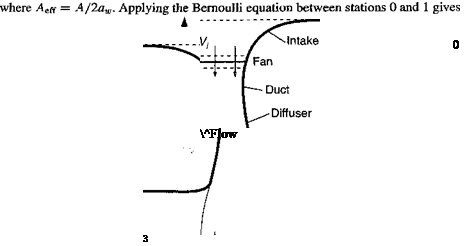
Figure 6.36 Flow model assumed for fan-in-fin analysis using momentum theory.

The theoretical analysis of the ducted rotor (propeller or fan) has been approached by Kruger (1949) and Kuchemann & Weber (1953), with experimental work by Mort (1965), and Mort & Gamse (1967). The momentum theory discussed in Chapter 2 can be extended to the analysis of a fan-in-fin design, with the flow model being shown in Fig. 6.36. Far upstream of the fan, the velocity can be assumed to be zero. At the plane of the fan, the induced velocity is u( . By the principle of conservation of mass, the mass flow rate, m, is constant through the system so that

m = pAvi = p(awA)w, (6.40)

where, by virtue of the duct design the area of the slipstream flow at the outlet is awA with the velocity at the duct outlet being w and with aw being a wake contraction parameter. This gives the relationship that w = Vi/aw. By means of conservation of momentum the thrust on the duct and fan is

T = 7duct + 7fan = mw = (pAvj)w =————–

aw

or

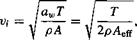
(6.42)

Po = Pi + – pvf,

and between stations 2 and 3 gives

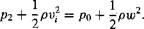(6.44)

Using Eqs. 6.43 and 6.44 gives for the thrust on the fan:

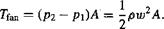(6.45)

Using Eqs. 6.41 and 6.45 gives

Tfan _ {pAw2 _ W _ 1

T pAviW 2 Vi 2 aw

Using Eqs. 6.42 and 6.46, we obtain the induced power consumed by the fan:

( T fcF Г3/2 (Pi) fan = TfnVi = — = —====

2awJV pA y/AawpA

(fi)fan

(Pi)rR

where (Рі)тя refers to a conventional (unducted) tail rotor. The latter equation gives an interesting result, in that it shows that if the shape of the duct is controlled so that the rotor wake does not contract as much as would occur naturally with a conventional tail rotor (for which in the ideal case, aw = 0.5, Aeff = A), less power will be required to produce a given total thrust. In the case where aw — 1 (the assumption of no wake contraction so that Aeff = A) a ducted fan of the same area will consume jpl of the power of a conventional tail rotor (i. e., 30% less power for the same net thrust). Alternatively, a ducted fan of half the disk area of a conventional tail rotor (i. e., a diameter reduced by a factor l//2) will produce the same thrust and consume the same power. Generally, however, because the length of the duct must be relatively short to minimize structural weight and drag penalties in forward flight, the potential gains in efficiency are not as large as suggested by the above analysis. Losses introduced by drive shafts also reduce any potential gains in efficiency. However,

4-It Л 1 ЛІ V!/>«• 1/ЧЛЛ л4¥/л<-л Л Л ПЛ/Ч1 (if r«4 TTHfL n 1 1Л Г 4/401 /VM /VII Г/4 n A1 »4І4 Q«" /-lll/tfl 1-4*4 ■■

ню luwti tip-uj&a diccta d^duudi&u vvitii a lau-iii-un givt; a iuivu^i ltuuuuuu ш induced power requirements. Overall, the fan-in-fin design offers some overall advantages compared to a conventional tail rotor for anti-torque and directional control.

The fan rotor design may also be approached from the principles of the blade element momentum theory (BEMT) discussed in Section 3.3. Equating the contributions to section thrust made from the momentum and blade element theories (using Eqs. 3.45 and 3.57), then we can write for the ducted fan that the incremental thrust is

2 1

dCj = —A2rdr = – crCir2dr, (6.49)

О-w 7

where the mass flow through the duct and fan is controlled by the effective wake contraction ratio aw. This is a function of duct design as well as the gap between the fan blades and the duct. Stator vanes are usually used to straighten the outlet flow and recover swirl losses, which are higher because of the higher rotor rpm. With the assumption for a value for aw (a common assumption for a fan is to use aw=1.25), then the inflow X can be solved by finding a solution to a modified form of the inflow equation, namely

Clearly, the optimum blade twist for a fan is of the same hyperbolic form needed for an unducted rotor. In some cases fan rotor designs may have large blade twist angles compared to a conventional tail rotor, and it may be inadequate to assume small angle approximations to find X. In this case the inflow equation can be solved numerically. Starting from Eq. 6.49 then the inflow distribution over the disk can be found using

X(r) = – y/awo(Ci cos ф — Cd sin0)r/4.

Because Ci and Q are functions of the blade section angle of attack, 9 —ф, which is in turn a function of X at each section, then the foregoing equation must be solved iteratively. Con­vergence, however, is found to be rapid. Thereafter, the sectional airloads can be determined and net rotor thrust and power follows by radial integration along the blade.

In forward flight the fan-in-fin is shielded from the external flow and the main rotor wake and, consequently, its performance is usually more predictable. Although as shown by Basset & Brocard (2004), even here empirical corrections to the momentum theory approach must be used because of the streamline inlet distortion produced by the duct. The vertical fin surrounding the fan is designed to provide a side force in forward flight and so most of the anti-torque. The aerodynamics of “sense of rotation” and the interference effects of the fin assembly, which are important for conventional tail rotors, are less important for the fan-in-fin design. However, the possibility of flow separation at the inlet lip of the shroud must be kept in mind, and usually the lip is carefully contoured to avoid such effects. Flow separation at the inlet to a ducted fan-in-fin can lead to a loss of thrust and/or thrust fluctuations that is consistent with some loss of effectiveness as a directional control producing device (instantaneous thrust) although not necessarily as an anti-torque device (average thrust).

From a safety perspective, the shrouded nature of the fan-in-fin reduces the possibilities of blade strikes during low-altitude flight operations and also the risk of injury to personnel on the ground. The larger number of blades on a fan-in-fin design increases the frequency of the rotor noise and this can appear in the helicopter noise spectrum over a range of frequencies to which the human ear is more sensitive. However, at greater distances these higher frequency sounds are more readily absorbed in the atmosphere. Efforts to reduce the noise of fan-in-fin designs through phase modulation using unequal blade spacing have made the fan-m-fin sound subjectively less noisy — see Vialle & Arnaud (1993).