Range flying – effects of wind

If the flight is to be made from A towards В and back to A, then wind of any strength from any direction will adversely affect the radius of action. This fact, which at first sounds rather strange, but which is well known to all students of navigation, can easily be verified by working out a few simple examples, taking at first a head and tail wind, and then various cross-winds. But the wind usually changes in direction and increases in velocity with height, and so a skilful pilot can sometimes pick his height to best advantage and so gain more by getting the best, or the least bad, effect from the wind than he may lose by flying at a height that is slightly uneconomical from other points of view. It may pay him, too, to modify his air speed slightly according to the strength of the wind, but these are really problems of navigation rather than of the mechanics of flight.

Flying for endurance – propeller propulsion

We may sometimes want to stay in the air for the longest possible time on a given quantity of fuel. This is not the same consideration as flying for maximum range. To get maximum endurance, we must use the least possible fuel in a given time, that is to say, we must use minimum power. But, as already explained, power means drag X velocity, the velocity being true air speed. Tet us look back to Table 5.2 showing total drag against air speed; mul­tiply the drag by the air speed and see what happens.

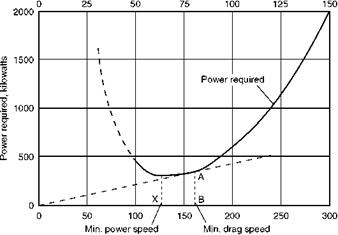
Table 5.2 shows that, although the drag is least at about 160 knots, the power is least at about 125 knots (see also Fig. 5.11, overleaf). The expla­nation is quite simple; by flying slightly slower, we gain more (from the power point of view) by the reduced speed than we lose by the increased drag. Therefore the speed for best endurance is less than the speed for best range and, since we are now concerned with true speed, the lower the height, the better.

The endurance speed is apt to be uncomfortably low for accurate flying; even the best range speed is not always easy and, as neither is very critical, the pilot is often recommended to fly at a somewhat higher speed.

The reader who would like to consider endurance flying a little further should look back to The Ideal Aerofoil in Chapter 3. Among the desirable qualities was a high maximum value of C j^/CD – the quality which means minimum power, i. e. maximum endurance.

There we were considering only the aerofoil, and the aeroplane is not quite the same thing as regards values, but the idea is the same. So for endurance flying we must present the aeroplane to the air at the angle of attack that gives the best value of C jjCD (for the aeroplane), and this will be a greater angle of attack and so a lower speed, than for range.

Fig 5.11 Flying for maximum endurance. Maximum endurance is at speed of minimum power (Л). Maximum range (minimum drag) is at speed В since AB/OB = Power/Speed = (Drag x Speed)/Speed = Drag, and AB/OB is least when OA is a tangent to the power curve.