Self-Similar Laminar Boundary Layers

Most finite-difference methods for solving the boundary layer equations (4.21), to be summarized in Sec­tion 4.10.2, actually solve transformed versions of these equations. One example is the following transfor­mation n, u ^ p, U using the local normal-length and streamwise-velocity scales 5(s) and ue(s).

The local length scale 5(s) can be chosen arbitrarily. However, it is advantageous to define it such that it is roughly proportional to the physical thickness of the boundary layer, so that the s-p computational grid grows along with the layer, as shown in Figure 4.11 on the left. This makes the U(s, n) velocity profiles stay within the s-p grid, which considerably simplifies the finite-difference solution procedure when it is applied on this grid, instead of on the physical s-n grid.

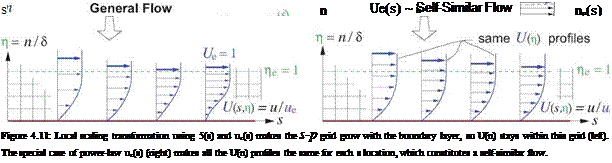One practical complication of the length scale choice 5 = ne shown in Figure 4.11 is that the boundary layer’s edge location is somewhat subjective, since u approaches ue only asymptotically. Alternative choices for 5 are 5[2], в, etc., which have the advantage of being unambiguously defined.

Another feature of the transformation (4.51) is that it fundamentally simplifies the problem for a special class of incompressible laminar boundary layer flows where ue(s) has a power-law form,

= Csa

we have the Falkner-Skan Transformation [12], [11]. The resulting transformed boundary layer equations no longer have any dependence on s, so their solution has the form U = U(n;a). This is called a self-similar boundary layer flow, in that all the velocity profiles are “similar,” or more precisely they have the same normalized U(n) at each streamwise location s. The situation is pictured in Figure 4.11 on the right. The U(n) shape does depend on the power-law exponent, however, so we get a different flow for each value of a.

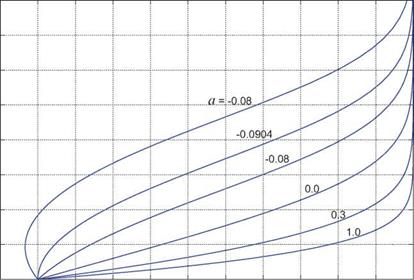
The Falkner-Skan solution velocity profiles are shown in Figure 4.12 for several values of a. Their numerical parameter values of interest are listed in Table 4.1. Note that because 5FS is significantly smaller than the boundary layer thickness ne, the n values are considerably greater than unity.

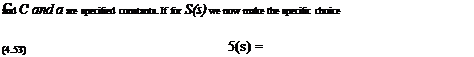8 7 6 5

n = n I Sfs 4

3

2

1

0

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

U = u I ue

Figure 4.12: Falkner-Skan velocity profiles, for several values of ue ~ sa power-law exponent a.

Each U(n) profile describes the entire self-similar velocity field u(s, n;a), via (4.51), (4.52), (4.53).

Numerical parameter values of interest for these profiles are listed in Table 4.1.

Although these solutions apply only to self-similar (power-law) laminar boundary layer flows, they reveal a number of important characteristics which apply to more general laminar boundary layer flows. They also confirm the general effects of pressure gradients which were qualitatively examined in Section 4.4. •

• The small minimum achievable negative value of amin = -0.0904 indicates that laminar flows cannot tolerate significant adverse pressure gradients, or equivalently, significant decreases in ue(s). For example, over a doubled laminar run distance, s2/s1 = 2, the minimum tolerable velocity decrease is ue2/uei = (s2/si)“min = 0.939 which is only a 6.1% deceleration.

a	8* 8fs	в 8vs	H	H*	ft*3 f	Rflxcv	A	r	Fe
2.00000	0.47648	0.21775	2.18820	1.63101	1.71507	0.97666	0.09483	0.37345	-0.04742
1.00000	0.64790	0.29235	2.21622	1.62575	1.23259	0.71291	0.08547	0.36034	0.00000
0.60000	0.79760	0.35483	2.24783	1.62006	0.97532	0.57484	0.07554	0.34608	0.05036
0.30000	1.01961	0.44196	2.30702	1.61009	0.72574	0.44474	0.05860	0.32075	0.13672
0.10000	1.34787	0.55660	2.42161	1.59308	0.49657	0.33251	0.03098	0.27639	0.27882
0.00000	1.72080	0.66412	2.59109	1.57259	0.33206	0.26109	0.00000	0.22053	0.44105
-0.05000	2.11777	0.75148	2.81815	1.55196	0.21348	0.21867	-0.02824	0.16043	0.59294
-0.08000	2.67173	0.82973	3.22000	1.52916	0.10155	0.19031	-0.05508	0.08426	0.74351
-0.09043	3.49786	0.86814	4.02916	1.51509	0.00000	0.18014	-0.06815	0.00022	0.82179
-0.08700	4.14726	0.84989	4.87975	1.52470	-0.04678	0.18303	-0.06284	-0.03976	0.78515
-0.08000	4.75540	0.80734	5.89021	1.55216	-0.07361	0.18800	-0.05214	-0.05943	0.70399

Table 4.1: Falkner-Skan solution parameters for self-similar boundary flows with ue(s) = Csa. The local Reynolds number is Rex = ue(s) s/v. Parameters A, T, Fe will be defined in Section 4.11.1.