Steady Flow

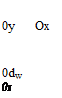Under steady flow conditions the terms involving time derivative vanish in Eq. 4.3b and, since the pressure difference at the wake is zero, the spanwise vortex sheet strength at the wake also vanishes, i. e., yw = 0. This results in the continuity of the vortices

Equation 4.7b dictates that dw is only the function of y. At the trailing edge the Kutta condition imposes the following restriction on the chordwise component of the vortex sheet

dw(x, y) = dw(xt, y) = da(xt, y)

which means its value is constant along x at a constant spanwise station. If we integrate Eq. 4.7a with respect to x and differentiate the result with respect to x, the Leibnitz rule gives the following for the chordwise component of the surface vortex sheet strength

Xt Xt

0ya d dx/ dxt

da(xt, y) = Oydx + 0 = dy 7adx + Уа(x/; У)dy _ 7a(x‘; У)"dy

x/ x/

The last two terms of the last expression vanish because of the character of the vortex sheet. Only contribution comes from the first term which is the derivative of the bound circulation to give

dw(y) = da(xt; y) = (4.8)

dy

Equation 4.8 tells us that the wake vorticity has a component only in stream wise direction and its strength varies with the bound circulation. The downwash expression then reads as