Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Supersonic Turning: Prandtl-Meyer Expansion and Isentropic Compression
The basics of fluid mechanics tell us, that supersonic flow will be accelerated (expanded), if the characteristic cross-section of the flow-domain is enlarged, and decelerated (compressed), if it is reduced. We call this expansion or compression by supersonic flow turning, see, e. g., [4].
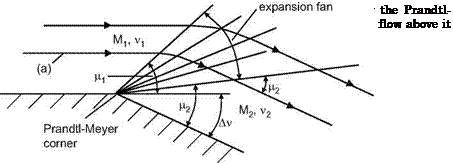
Supersonic flow turning implies that small turning rates are involved, with basically isentropic changes of the flow. The Prandtl-Meyer expansion is an isentropic flow phenomenon in which the flow speed is increased. In a sense it can be considered as the counterpart of an oblique shock wave, where the flow speed is reduced. However, across the shock wave we have a discontinuity of speed, whereas with the Prandtl-Meyer expansion a gradual increase of the flow speed occurs.
The Prandtl-Meyer expansion is a “centered” expansion phenomenon, Fig. 6.25. Downstream of the expansion fan the flow again is parallel to the body surface. If a streamline (a) in the expansion fan is selected as a body contour, we have above it a “simple” expansion. However, in such a case the hidden Prandtl-Meyer corner can be used to describe the flow. The Laval – nozzle expansion between nozzle throat and contour inflection point, Fig. 5.7, can be considered as an example of such a simple expansion.
The real counterpart of the Prandtl-Meyer expansion is the isentropic compression of supersonic flow, which can be envisaged, for example, as the inverse flow in a Laval nozzle. Investigations have been made whether isen – tropic compression can be used in supersonic engine flow inlets [9]. Such a flow can be imagined as a compression by an infinite number of very weak shocks. In practice, however, such flow would be very sensitive to contour disturbances—the boundary layer already is such a disturbance—so that isen – tropic compression is considered today as not feasible.
Supersonic flow turning of a perfect gas is described by an expression obtained from eq. (6.116) for small ramp angles 5 (for the derivation see,
e. g., [4]):
Here S is the deflection angle and V the resultant flow velocity. Integrating this expression gives the Prandtl-Meyer angle v(M)
-6 + c= j /M2-ly = i/(M). (6.131)
After further manipulation we obtain the following relation for v(M)
 |
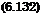
.1/’ I dM
 |
 |
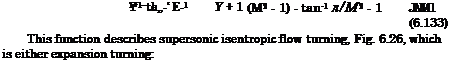This relation integrated yields the Prandtl-Meyer function [3, 4, 11]:
v = vi + |S — Si I (6.134)
or compression turning:
v = vi — |S — Si I. (6.135)
Av can be computed as a function of Mi and y directly from eq. (6.133). No explicit relation is available to find the resulting Mach number for a given Prandtl-Meyer angle. An iterative solution procedure can be programmed.
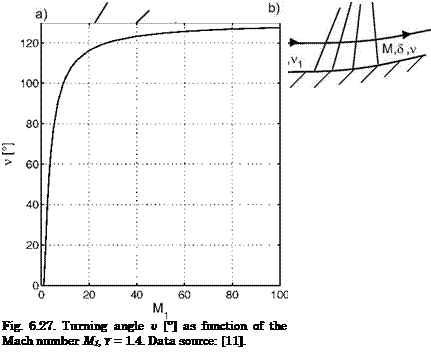
Tabulated data for M and v for y = 1.4 can be found in [11]. In Fig. 6.27 we give the turning angle v [°] as function of the Mach number Mi for Y = 1.4.
 |
Since both expansion and compression turning are isentropic, the relations given in Section 6.2 can be used to determine pressure, temperature and the like.
 |
 |
 |
We consider now supersonic isentropic flow turning at very large Mach numbers. In such cases /M2 — 1 « M, and eq. (6.133) reduces to
|
– – — +0{M-3) 2 M v ; |
The largest possible expansion turning angle is that, for which V2 = Vm. One has to keep in mind, that Vm is finite, eq. (6.15). If it is reached, T2 = 0 K, and hence M2 ^ ж. Because the Prandtl-Meyer relation is formulated in terms of the Mach number, we cannot determine from it the maximum expansion turning angle. The largest possible compression turning angle is that which leads to M2 = 1.
With these results we have attained insight into the two turning phenomena, of which the Prandtl-Meyer expansion is the more important one. However, it does not find a direct application in computation schemes, except for the shock-expansion scheme [4], which is used in approximate computation methods for aerothermodynamic loads determination, see, e. g., [34].
We finally give examples for expansion and compression turning in Table 6.6. It is interesting to observe that for Mi = 20 despite the large Mach number changes (M2) with the given turning angle for expansion only a small velocity (V2 ) change occurs. The static pressure P2 however reacts strongly, less strongly the temperature T2.
|
Table 6.6. Supersonic isentropic turning: examples of expansion and compression turnings.
|
