The simplified horseshoe vortex

A simplified system may replace the complete vortex system of a wing when con­sidering the influence of the lifting system on distant points in the flow. Many such problems do exist and simple solutions, although not all exact, can be readily obtained using the suggested simplification. This necessitates replacing the wing by a single bound spanwise vortex of constant strength that is turned through 90° at each end to form the trailing vortices that extend effectively to infinity behind the wing. The general vortex system and its simplified equivalent must have two things in common:

(i) each must provide the same total lift

(ii) each must have the same value of circulation about the trailing vortices and hence the same circulation at mid-span.

These equalities provide for the complete definition of the simplified system.

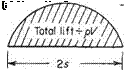The spanwise distributions created for the general vortex system and its simplified equivalent are shown in Fig. 5.14. Both have the same mid-span circulation Го that is now constant along part of the span of the simplified equivalent case. For equivalence in area under the curve, which is proportional to the total lift, the span length of the single vortex must be less than that of the wing.

Thus

Го2/ = area under general distribution = ^

pV

Hence

s’ total lift s 2spVTo

2У is the distance between the trailing vortex core centres. From Eqn (5.47a) (see page 246) it follows that

L = pV[24] [25]s2‘2ivA

and substituting also

Го = 4sVEA„ sin и

У рУ^^тгАї s 2pV24sP-Y^A„ sin и I

7Г A 4 [Ai-A3 + A5-A7…}

For the general case then:

For the simpler elliptic distribution (see Section 5.5.3 below):

A3 = А3 = Ат = 0

(5.18)

In the absence of other information it is usual to assume that the separation of the trailing vortices is given by the elliptic case.