Three Dimensional Boundary Layers
Consider a flat wing, away from the tips, at zero angle of attack in incompressible flow. The boundary layer equations are
![]() du dv d w
du dv d w
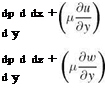 |
||
dx + d y + dz
The same result can be found that ~ 0, hence the pressure is given by the inviscid flow solution.
The boundary conditions at the solid surface are u = v = w = 0.
At the outer edge of the boundary layer, u = ui and w = wi. The v-component at the edge carries the influence of the boundary layer on the inviscid flow. It is not known a priori and is part of the solution.
The initial condition, upstream of the wing is simply uniform flow u = UOT.
For infinite swept wings with the z-axis in the direction of span (Fig. 8.12)
![]() d p du dw
d p du dw
 |
dz = dz = dz
hence, the boundary layer equations reduce to (p = const.)
![]() du dv
du dv
dx + d y ^
![]() dw dw d2w
dw dw d2w
pu dx + pv dy = ‘‘ay?
Note that u and v are independent of w, the so-called independence principle. This is true only for incompressible flow where p = const.
The general three-dimensional boundary layers are covered in Howarth [4] and Stewartson [6]
Finally, the sources of the fundamental materials in this section are reviewed. The analysis of the relative motion near a point is discussed by Batchelor [7].
The theory of boundary layer is covered in Schlichting [3], Rosenhead [8] and White [9].
Applications to low speed aerodynamics are discussed in Moran [10]. Compressible viscous flows are studied in Liepmann and Roshko [2] and in Stewartson [6].
Stability of viscous flows as well as transitional and turbulent flows are not covered here and the reader is referred to literature for these topics.











