TWO-DIMENSIONAL THIN AIRFOILS IN A STEADY FLOW OF AN INCOMPRESSIBLE FLUID
Let us consider a strip of unit span of a two-dimensional thin airfoil as shown in Fig. 6.1. Let the origin of a right-handed rectangular coordinate system be taken at the leading edge of the airfoil profile. Let
![]() У
У
the x axis be taken along the chord line and the у axis be perpendicular to it. The airfoil camber line is described by the equation
у = Y(x) (0 < г < c) (1)
If a steady two-dimensional flow with speed U and an angle of attack a (at large distance from the airfoil) streams past the airfoil, disturbances are introduced into the flow by the airfoil in such a manner that the resultant flow is tangent to the airfoil. According to the aerodynamic theory, the thin airfoil can be replaced by a continuous distribution of vorticity (a vortex sheet). Let the strength of the vorticity over an element of unit length in the spanwise direction and dx in the chordwise direction be y(x) dx. The lift force contributed by the element dx is, according to Joukowsky’s theorem,
dL = pU y(x) dx (2)
The total lift per unit span is therefore
L = puj’y(x) dx (3)
where c is the chord length of the airfoil.
For a thin airfoil of small camber (y(x) < c), the surface of the airfoil differs only infinitesimally from a flat plate. The induced velocity over the airfoil surface, to the first order of approximation, can be calculated by assuming the vortices to be situated on the x axis. The у component of the induced velocity at a point x on the x axis is*
which, to the first order of approximation, is the same as the component of velocity normal to and on the airfoil surface at the chordwise location x.
The slope of the fluid stream on the airfoil is then a + This must be
equal to the slope of the airfoil surface dY/dx. Hence, the boundary condition on the airfoil is
![]() v{ dY <x + — — – j – V dx
v{ dY <x + — — – j – V dx
The vorticity distribution y(x) must be determined from Eq. 5. In addition, the Kutta condition that y(c) = 0 must be satisfied, which is equivalent to the statement that the fluid must leave the trailing edge smoothly.
* This is a Cauchy integral. See footnote on p. 126.
In place of x let a new independent variable ip be introduced so that
When x varies from 0 to c along the chord, ip varies from 0 to it. The vorticity distribution can be written as*
Substituting (7) into (4), we obtain (see Ref. 1.43 for details)
![]() / Xа
/ Xа
V{ = и 1 – A0 + > An cos nip Equation 5 then implies
CO
![]() oc — A0 + An cos nip
oc — A0 + An cos nip
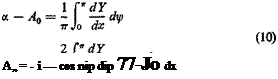 |
The left-hand side is a Fourier series. The coefficients can therefore be determined by the usual method. Multiplying Eq. 9 by cos nip {n = 0, 1, 2, • • •). and integrating from 0 to it, we obtain
From Eqs. 3 and 7, the total lift can be obtained. The result, expressed as the lift coefficient, is
Cz = n(2A0 + A1) (11)
Similarly, the moment about the leading edge, expressed as the moment coefficient, is
(СлАе. = — (л0 + At – І л) = -1 (Аг – АД — CL (12)
A substitution of Eq. 10 into Eqs. 11 and 12 gives
CL = 2тг(а + £0) (13)
(СдЛ. е. = (/Mo —’ 2 e°) ~~ 4 (14)
A form assumed by H. Glauert.1-43
1 dY
£o = ~ ~ – г – (1 – cos y>) dy>
77 Jo UX
Л-~2І г(і-“*ад^
From Eq. 13 it is seen that £0 is the negative of the angle of zero lift and that the theoretical value of dCL/da. is In. The experimental value of dCJda. is somewhat smaller than 2w. It is convenient to write Eq. 13 as
= + є o) (16)
From Eq. 14 it is seen that fi0 — – e° is the moment coefficient at zero
lift and that the lift force acts through the 1/4-chord point (the aerodynamic center). The coefficient of moment about a point at a distance x from the leading edge is
(C. m)x = (СлЛе. + j CL (17)
Differentiating, we obtain
![]()
_ dCL da. dot
Equation 15 shows that, for an airfoil with parabolic or circular camber, the lift is determined by the slope of the camber line at the 3/4-chord point. For such an airfoil can be described by the equation
у = Y(x) = ax(c — x) (19)
where ac2/4 is the maximum camber at the mid-chord point. Hence,
dY о
— = ac — lax — ac cos w dx
So, when x = 3c/4, dY/dx — — ac/2. Now, from Eqs. 15, (20)
1 f” ac
— e0 — — ac cos ip( 1 — cos y>) dy> = ——
TT Jo 2
which is exactly the value of dY/dx at the 3/4-chord point. Therefore the line of zero lift is parallel to the tangent to the airfoil at the 3/4-chord point.
Since the resultant lift force acts through the 1/4-chord point, the vorticity can be regarded as concentrated there in calculating the lift.
The downwash due to a concentrated vortex of strength Г located at the y4-chord point is
____ = пі)
2тг{ф-х) 2тт{ф-х)Ри 2(1/4-ж/с) v
At the 3/4-chord point, x/c = 3/4, we have
– і (»<>»-,. -* + «.-*- (£)„_. СЩ
In other words, if the vorticity is considered as concentrated at the aerodynamic center (1/4-chord point), the boundary condition for downwash is satisfied at the 3/4-chord point.
We have quoted in § 4.3 that, for a swept or unswept wing of finite span, if the lifting line (the vortex line) is located at the ^-chord line and the downwash condition is satisfied at the 3/4-chord line, the result will give a good approximation to the spanwise lift distribution (Weissinger’s method). Thus the 3/4-chord line seems to have a unique importance. We shall see later that this line is also uniquely significant for oscillating airfoils.













