Viscosity effects

4.5 We have already noted many times, especially in Sec­tion 2.4, what a vital part is played by the effects of viscosity and by vis­cous interactions in the flows which interest us in aircraft design, even if the flows remain attached to the surface of the wing up to the trailing edge. Therefore, no theory for determining the properties of classical and swept wings is complete if it cannot take proper account of the effects of viscosity. In this Section, we want to discuss briefly what the main effects are and indicate how far they may be predicted. We shall be concerned throughout with rather rough approximations since solutions of the complete Navier-Stokes equations for. compressible flows are not yet available for our design purposes.

We consider flows where the viscous region may be thought of as a thin boun­dary layer near the wing surface and as a thin wake downstream of the wing.

In the first place, this implies that skin-friction forces act along the sur­face of the wing, which have a counterpart in a loss of momentum in the wake far behind the wing. Further, on a lifting wing, the streamlines in the re­gion of the trailing edge must be inclined to the direction of the mainstream and thus the wake will be curved as it turns back into the mainstream direc­tion. This curvature implies that there is a circulation in the viscous wake, i. e. a vorticity component across the mainstream, in addition to the stream – wise vorticity component (see e. g. G I Taylor (1925), G Temple (1943), and J H Preston (1949) and (1954)). This circulation must be taken into account when the lift is derived from Trefftz-plane considerations and, since it is usually negative, the actual lift is less when the wake is included than when it is ignored. Lastly, the boundary layer displaces the streamlines in the external inviscid flow outwards away from the body, as already discussed in Section 2.1, and the pressure along the surface of the given wing may be taken to be the same as that in a hypothetical inviscid flow along the displacement surface, obtained by adding the displacement thickness of the boundary layer and of the wake of the wing, as explained by M J Lighthill (1958) and К Gersten (1974). This has the effect of changing the pressure distribution over the wing surface everywhere from that calculated for an inviscid flow.

What are needed by the designer are methods for estimating all these effects, which are rapid, accurate and adaptable, and which can be regarded as routine tools. In particular, it should be possible to assess the effects of small changes in the wing shape and also to work out the properties of threedimen­sional wings at full-scale Reynolds numbers. We shall find that we are still far from having reached such a position.

In view of the complexity of the problem, we are more than ever interested in making simplifying assumptions. Boundary-layer assumptions may be made in the estimation of some of the effects. But boundary-layer methods use con­cepts which are essentially associated with flows past flat plates, and there are several regions in the flows past wings where the flow differs signifi­cantly from that along a flat plate, and where at least higher-order approxi­mations should be considered. One such region is that near the leading edge where the flow is highly curved. Here, fortunately, J C Cooke (1966) could show that the curvature effects may justifiably be ignored in most practical cases. In this work, second-order terms were taken into account and Cooke found that, on convex surfaces, the skin friction is reduced and the displace­ment thickness increased, as compared with first-order solutions. Cooke’s method is of special interest in that the displacement surface is supposed known and the body surface determined by working inwards. This method has been used by D Catherall & К W Mangier (1963), and it may have further applica­tions in wing design.

Matters are different in the region near the trailing edge, including the near­wake. The flow is very complex and cannot be properly described by standard boundary-layer concepts even in the case of a flat plate with a trailing edge (see К Stewartson (1968) and (1969), N Riley & К Stewartson (1969)). In the case of lifting wings with non-zero trailing-edge angles, the curved flow is even more complicated, and changes of the pressure through the boundary layer and the near-wake are an essential feature, not only in viscous flows but also already in an inviscid, rotational model of the flow (see Section 2.4, Fig.2.3X Thus the Kutta condition, however useful in inviscid flows, is inadequate and ill-defined in viscous flows, especially in three dimensions, but we do not yet know with any certainty what to replace it by. In principle, it should be replaced by a suitable condition applied at all points along the boundary representing the wake. But this has not yet been worked out and incorporated in any method, and this renders the determination of the pressures at and near the trailing edge and of the circulation rather uncertain. It would be well worthwhile if someone would turn his attention to this fundamental problem rather than producing yet another panel or relaxation method.

To estimate the effects of boundary layers, we must calculate them first. There is a vast number of particular methods for calculating the development of boundary layers, accumulated over more than 70 years of intensive research (see e. g. the textbooks by H Schlichting (1960), L Rosenhead (1963), and A Walz (1966)). Here, we are interested in methods which can deal with three­dimensional flows. L Prandtl (1945) and W R Sears (1948) and (1954) were the first to provide methods for infinite sheared wings, exploiting the similarity characteristics inherent in this particular curved flow. More general methods followed (see e. g. N Rott & L F Crabtree (1952), J C Cooke & M G Hall (1960),

R C Lock (1967), J C Cooke & J H Norbury (1967), В G J Thompson et al. (1973),

E H Hirschel (1973), J A Beasley (1974), M T Hill & H-J Wirz (1974)), and lami­nar threedimensional boundary layers can now be calculated with some accuracy (see e. g. E Krause (1969) and (1973), E Krause et al. (1969), P Bradshaw

(1971) , N A Jaffe & A M 0 Smith (1972), E A Eichelbrenner (1973)), provided the external flowfield is well-defined and known. Some of these methods con­tain empirical elements and apply also to turbulent flows.

In recent years, numerical solutions of the Navier-Stokes equations for vis­cous compressible flows have been computed. A review of this work ahd a use­ful list of the flows treated so far have been provided by R Peyret & H Viviand (1975).

The next step is to determine where and how transition from the laminar to the turbulent state occurs. On threedimensional swept wings, there are now six known mechanisms which may bring about transition and several of these may operate simultaneously (see e. g. M G Hall (1971)). These have recently been reviewed by D A Treadgold & J A Beasley (1973) and by E H Hirschel (1973) and applied to several typical cases of infinite sheared wings with different sec­tion shapes, with rather alarming results: it turned out that it is very dif­ficult to predict which of the various mechanisms is likely to dominate, for any given shape and Reynolds number, and uncertainties were revealed which are far too great for engineering purposes; to narrow them down needs much fur­ther work. The results also indicate that the flow itself can be so sensitive that it depends on the fine detail of the pressure distribution and of the wing shape so that the demands on the accuracy of any theory are very high. As a consequence, present estimates of the transitional flow regime on swept wings, and the input into any calculation of the development of the turbulent bound­ary layer and especially its initial conditions, must be regarded as poor and unreliable.

Of the many methods for calculating turbulent boundary layers, we mention only a few more recent methods which have proved useful in practical applications:

J C Rotta (1962) , D В Spalding & S W Chi (1964), N A Cumpsty & M R Head (1967), M R Head & V C Patel (1969), R Michel et al. (1969), H Femholz (1969),

P Bradshaw & D H Ferris (1971), P Wesseling & J P F Lindhout (1971), J E Green

(1968) , J E Green et al. (1972), P D Smith (1972), E Krause (1973), and the extensive text about twodimensional and axisymmetric turbulent boundary layers by T Cebeci & A M 0 Smith (1975). Existing methods have been assessed by

5 J Kline et at. (1968) for two dimensions, and by L F East (1975) for three. The methods are generally of one of two forms: finite-difference methods in which the governing partial differential equations are solved numerically; and integral methods in which the partial differential equations are reduced, by an integration in the direction normal to the surface, either to a set of ordin­ary differential equations, if the flow is twodimensional, or, if the flow is threedimensional, to a set of partial differential equations involving only two independent variables. Both forms involve considerable empiricism to ren­der the equations determinate. For the predictions of threedimensional boun­dary layers, which interest us here, streamline coordinates are often used, which consist of two families of mutually orthogonal curves on the surface of the body. One family is formed by the projections onto the surface of the curved streamlines just outside the boundary layer. The direction of such an external streamline is called the streanwise direction, and the crossflow is then normal to an external streamline and parallel to the surface. An essen­tial assumption in many of these methods is that the streamwise flow is simi­lar to that of a corresponding twodimensional boundary layer, which is suppor­ted by some experimental evidence. But the streamline coordinate system is inconvenient for practical purposes since it changes with the general flow conditions over the wing, and a curvilinear coordinate system fixed in the wing surface is more useful, even though it will, in general, be non-orthogo­nal. Now D F Myring (1970) has shown that the observed similarities with two­dimensional flows can be exploited even when a coordinate system is adopted which is not based on external streamlines, and P D Smith (1972) has subse­quently provided a numerical method which is flexible and well-adapted to prac­tical needs.

Because all these methods involve a strong empirical element, it is important to have good experimental evidence for relevant flows. Although this is well recognised, there is, nevertheless, a dearth of reliable and complete data and we can refer here only to a few sets of measurements: by G G Brebner & J A Bagley (1952) and T A Cook (1971) on twodimensional aerofoils; by G G Brebner (1950), (1954), and (1960), В van den Berg & A Elsenaar (1972), К G Winter &

J В Moss (1974), and В van den Berg et at. (1975) on swept wings; and by M G Hall A H В Dickens (1966), К G Winter, J C Rotta & К G Smith (1968), L F East

6 R P Hoxey (1969) on more specific threedimensional flows. Most of these measurements are not quite complete enough to give all the data needed to check all the assumptions made in the various theories and these, therefore, remain tentative to some degree.

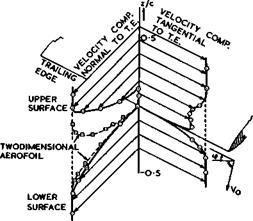
There are some general characteristics of thT^eedimensionat boundary layers over swept wings which follow from the pattern of curved streamlines sketched in Fig. 4.6. Physically, it is the transverse pressure gradient in the external stream which produces the secondary crossflow in the boundary layer: the reduction in velocity in approaching the surface results in a decrease in the centrifugal force which, outside the boundary layer, is in equilibrium with the transverse pressure gradient. Since the static pressure remains approximately constant through the boundary layer, the curvature of the stream­lines in the boundary layer must be increased as the wall is approached and the velocity reduced, to restore the centrifugal force to its required value (see also Fig. 2.5). This causes a transport of fluid towards the concave side of the external streamlines. The similarity of the velocity profiles to those in twodimensional flow, which has been mentioned above, strictly applies only to laminar boundary layers along the developable surfaces of sheared wings of infinite span. The boundary layer equations then reduce to a simple form where the solution for the velocity components in planes normal to the direction of sweep is the same as in the corresponding twodimensional case, so that a solution for the spanwise velocity component can be obtained inde­pendently by substituting the known solution for the normal components. This has been called the independence principle by R T Jones (1947). It cannot strictly apply either to turbulent boundary layers or to threedimensional wings. On a sweptback wing, the curvature of the streamlines and with it the crossflow will build up gradually away from the centreline, and the thickness due to crossflow will increase towards the tips. Thus, here again, there is a centre effect in that the rate of build-up of the crossflow (with y) is large in the central region and then becomes more gradual where sheared-wing conditions apply. The direction of the velocity vector will always reach the largest deflection from the mainstream direction at the limiting stream­lines in the wing surface. Another limit is reached when the limiting stream­lines in the surface are turned completely into the spanwise direction. As has been discussed in connection with Fig. 2.5, this may be interpreted as a separation of the flow component normal to the direction of sweep. In such a flow, the independence principle cannot possibly hold and there need be no similarity to any twodimensional flow. The separation line may be an ordinary separation line and lead to the formation of a vortex sheet extending into the external inviscid stream (see Fig. 2.7). Alternatively, the separation streamsurface may stay immersed in the viscous region. Where a bubble with

Fig. 4.27 Boundary-layer profiles at the trailing edge of a wing with 45° sweepback. After Brebner (1954)

an initial reversed flow behind the separation line might have been formed in a twodimensional flow, with subsequent reattachment to the surface, such a would-be bubble on a swept wing might be "filled in" immediately by air flow­ing sideways into it from parts of the wing further inboard and upstream. The flow does not then reattach to the surface but to a sublayer with predominantly

spanwise flow. Velocity profiles may then look like those in Fig. 4.27, as measured by G G Brebner (1954), with a nearly uniform sublayer of spanwise outflow underneath another layer which does not appreciably differ from that on a twodimensional aerofoil with a comparable pressure distribution. More intense turbulent mixing might efface the features so sharply displayed in Fig. 4.27 and lead to more blurred velocity profiles. It can then be expected that the actual flow will depend strongly on the Reynolds number as well as on the lift coefficient and the angle of sweep. Generally, the thickening of the boundary layer through outflow, with all its consequences, must be expect­ed to increase towards the wing tips and with increasing and angle of

sweep. This will be confirmed below.

The first important effect caused by the existence of the boundary layer is a drag force, which is to be added to the vortex drag and is often referred to as profile drag (for a detailed derivation of this drag force see e. g. В Thwaites (1960) and W J Duncan, A S Thom & A D Young (1970); see also Section 3.2). This consists of two parts: the skin-friction drag which can be deter­mined directly from the boundary layer, once its development along the sur­face has been calculated; and the pressure drag, or form drag, which can be de­termined by integrating the streamwise component of the pressure around the surface of the wing. This form drag is zero in inviscid subcritical flow and becomes non-zero in viscous flow when the pressure on the wing is worked out as that on the displacement surface. The profile drag is often assumed to be independent of the lift; it is then identical with the zero-lift drag Cpp in (3.42).

There are many methods for obtaining rapid, but approximate, predictions of the profile drag of twodimensional aerofoils, beginning with those by J Fretsch (1938) and H В Squire & A D Young (1937). The latter found that the pressure drag is roughly t/c times the total profile drag. On infinite sheared wings, there is a sweep effect which tends to reduce the profile drag below that of the corresponding twodimensional aerofoil, as has been measured by J Weber &

G G Brebner (1952) and explained by J C Cooke (1964). But matters are much more complicated when the drag of real aircraft is to be predicted. For ex­ample, the surface cannot be assumed to be smooth and the effects of surface imperfections must be taken into account (see e. g. S F Hoemer (1965),

L Gaudet & К G Winter (1973)). Also on complete aircraft, a very large number of individual drag sources must be accounted for, and drag prediction for the appraisal of projects and for the estimation of an aircraft’s performance re­quires a very complex framework of techniques. This must be a process of syn­thesis, rather than a simple summation, and it is essential to know about the individual flow elements, and their interactions, which together constitute the complete flow pattern. For a survey of present drag prediction methods, we refer to two recent reviews by J H Paterson et al. (1973) and by S F J Butler (1973). In view of the complexity and magnitude of the task of deter­mining the drag of aircraft, it is not surprising that the available theoreti­cal methods are as yet. inadequate and that much has to be left to experiments.

The second important effect caused by the existence of the boundary layer and wake is the reduction of the lift force and associated changes in the pitching moment. That the viscous drag of an aerofoil reduces the lift force on it was first realised by A Betz & I Lotz (1932) who proposed a model of the flow where the boundary layer and wake are represented by a suitable distribution of sources over the surface of the aerofoil, adjusted to produce a displacement surface and the right overall viscous drag. Since the boundary layer on a. lift­ing aerofoil is, in general, thicker on the upper surface than on the lower surface, these sources are put on the rear part of the upper surface so that, in the simplest model, the source flow is bounded by two streamlines: one ori­ginating from the upper surface of the aerofoil just upstream of the sources, and the other from the trailing edge. Thus the Kutta condition of smooth out­flow from the trailing edge in inviscid flow is replaced by a condition which involves two streamlines leaving the aerofoil, with a source flow interjected, in this model of the viscous flow. It is then possible to explain why visco­sity leads to a reduction of the circulation. This model could be developed further (see e. g. J Pretsch (1938)) into a routine method for practical pur­poses, including threedimensional wings, but this has not yet been done successfully.

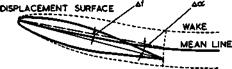
Another approach which has led to some success is that by J H Preston (1949) and (1954). It is based on a model illustrated in Fig. 4.28. The boundary of Fig. 4.28 Aerofoil with displacement surface superposed (schematic)

the displacement surfacg is shown schematically by adding the displacement thicknesses and 6^ , together with a new mean chordtine halfway between

the boundaries on the upper and lower surfaces. Thus the thickness of the aerofoil is increased by an amount.£(Sj + 6*) on either side of the new mean line and a wake is added; and the angle of incidence is changed by Aa and the camber changed by Af (both of which are usually negative); both of these are to be determined from J (6jJ[ – 6*). The mean line in the wake is curved and ehould be represented by a vortex distribution which changes the down – wash along the new mean line and reduces the circulation further. Again, this model of the flow explains clearly why the lift is reduced by the viscous drag.

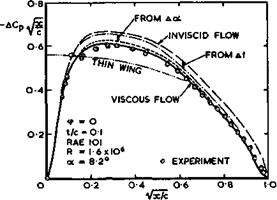
This model leads to a relatively simple method for estimating viscosity effects, which has been applied convincingly by G G Brebner & J A Bagley (1952) to a twodimensional aerofoil for which they also obtained careful pressure and boun­dary-layer measurements*). Using experimental results for 6*(x) and 6*(x), they calculated first the pressure distribution with the Kutta condition ful­filled at the midpoint on the meanline above the trailing edge. Then they used the results of J H Preston (1949) to reduce the circulation further in order to fulfil Taylor’s theorem that equal amounts of positive and negative vorticity should be shed into the wake. One of their results for the chord – wise loading, in Fig. 4.29, shows that these effects account quite well for the measured values. It also shows how the final calculated loading comes about: starting from the loading for the thin wing and going from there to that of the thick wing, both in inviscid flow, and subsequently accounting for the camber effect, Af, this being most noticeable over the rear of the section, and then for the effects of Да and of the reduction of circulation, which are taken as constant factors to ACp(x) in inviscid flow. This is roughly the sequence of effects to be borne in mind. Evidently, each of them matters and

*) These measurements also show interesting evidence on a possible effect of transition. At low angles of incidence, transition occurred at about midchord and took the form of a laminar separation bubble with reattachment, not of an instability. The bubble was very shallow and caused only a slight dip in the pressure distribution; the bubble length was about 0.2 c.

157

any theory which cannot take some account of all of them is of limited practi­cal usefulness.

Fig. 4*29 Experimental and calculated chordwise loadings over a two­dimensional aerofoil. After Brebner & Bagley (1952)

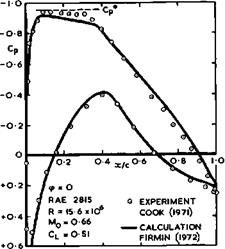
Strictly, this application of Taylor*s theorem is not sufficient, especially when the effect of the circulation in the wake is larger than in the example in Fig. 4.29, as it is on sections with significant rear loading. A better representation of the vorticity in the wake has been worked out by D A Spence & J A Beasley (1958), and attempts at achieving further improvements have been made by R C Lock et at» (1968) and (1970) and also by J Steinheuer (1973) who obtained results which represent the experiments of Brebner & Bagley very well, including the effects of changes in the Reynolds number. И С P Firmin (1972) has provided an iteration method for compressible subcritical flows, which proceeds in steps by calculating pressure distributions and boundary-layer and wake developments, using the framework of the RAE Standard Method for the for­mer and the entrainment method of J E Green (1972) for the latter. In the first step, the pressure distribution in inviscid flow is suitably adjusted

Fig. 4.30 Experimental and calculated pressure distributions over a two­dimensional aerofoil

LIVE GRAPH

Click here to view

The Aerodynamic Design of Aircraft

and changed rather arbitrarily in the region of the trailing edge to avoid any separation or divergence at this initial stage of the iteration. It is inter­esting to note that, to avoid divergence, it has also been found that only a proportion of the change in ordinates should be included during any one step, so that a relaxation factor had to be introduced and limited to 0.2. This means that the number of steps to be taken may be rather large. Thus Firmin’s may be regarded as an interim method, and subsequent developments may lead to improvements not only in the accuracy but also in the ease of obtaining a solu­tion, brought about by a better physical model of the flow. In the meantime, the results in Fig. 4.30 show that the main features of the pressure distribu­tion over a twodimensional aerofoil can be predicted very well, albeit not altogether satisfactorily.

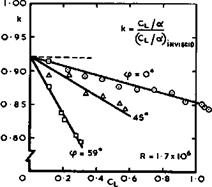
Fig. 4.31 Reduction of the sectional lift slope due to the boundary layer on a twodimensional aerofoil and near mid-semispan on two sweptback wings

The experimental results in Fig. 4.31 show how the effects of viscosity increase with increasing lift coefficient, using as a demonstrator the sectional ■lift slope as a fraction, к , of its value in inviscid flow. Evidently, not only the displacement thicknesses themselves but also the difference б* – 6* in­crease with Cl, so that к appears to decrease roughly linearly with in­creasing CL. Even in the limit Cl 0, the boundary layer reduces the lift slope well below the value in inviscid flow. Why this value should seem to be independent of the angle of sweep has not yet been explained. The lift re­duction goes together with a slight forward shift of the aerodynamic centre.

All the observations and theories described so far concern twodimensional flows. The concepts put forward about the displacement effects and the wake have proved fairly useful, but inadequacies in the numerical answers obtained from them are clearly apparent: in the determination of the drag and of the pressure in the trailing-edge region. Also, the extension of the Kutta condition to real flows presents conceptual difficulties. We must be prepared, therefore, to find that the treatment of viscous effects in threedimensional flows is rather more uncertain.

First conjectures, together with some experimental evidence, on the effects of viscosity on the type of flow over threedimensional swept wings are given in two papers by D KUchemann (1955), based in the main on concepts already des­cribed above. In view of the properties of threedimensional boundary layers, with their significant spanwise outflow on sweptback wings, viscous interac­tions must be expected to become much stronger when sweep effects make them-