Viscous/Inviscid Interaction Procedures Based on Domain Decomposition Techniques

In these zonal procedures, the flow field is divided into two regions. To patch the two regions, an overlap layer, where the equations on both sides are valid, must exist.

Quarteroni and Valli [37] studied direct coupling of the Euler and Navier-Stokes equations. The motivation is clear. Away from the body, the grid is usually coarse and the viscous terms are not resolved and are not needed anyway, hence they are switched off. It turns out that errors can be reflected at the interface. Some fixes are possible however, but the general case is complicated.

To demonstrate some of these ideas, we will use stream function/vorticity formu­lation for incompressible two-dimensional steady laminar flow. The Navier-Stokes equations in Cartesian coordinates are given by

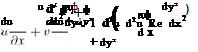where

The boundary conditions on a solid surface are given in terms of ф (u is unknown there), namely ф = const and дф/дn = 0, where n is the normal direction to the surface. For multi-connected domain, special treatment is required to assign the level of ф on each closed body.

For high Reynolds number flows, upwind differences are used for the convective terms of the vorticity equation. Moreover, thin layer approximations (or partially parabolized Navier-Stokes equations) may be used, where the second derivatives in the tangential direction of the main flow in the vorticity equation, uxx, is neglected.

Notice, neglecting i^xx compared to фуу as well, will lead to the boundary layer approximations and the equations become parabolic, where upstream effect is not possible. hence, the name of partially parabolized equations, where only uxx is neglected.

Obviously, the flow in the whole domain can be simulated using a stretched grid and iterative methods of the discrete equations coupled, for example successive line iteration can be used with 2 x 2 block tridiagonal solver, marching in the flow direction. Several sweeps are required for convergence.

Now, one can split the domain in two regions. in the outer one, vorticity vanishes and the vorticity equation is not needed. The question is where should the interface be? One can calculate the viscous terms, from the previous iteration, and if they are relatively small, they are switched off. Here, for convenience, the two regions are fixed a priori using rough boundary layer estimates.

To see the effect of switching off the vorticity in the outer region, the same numer­ical method described before for the whole domain is used. Comparison of accuracy of the results (i. e. friction drag) and the convergence of iterations for different sizes of the viscous region may assess the merit of this zonal approach (see Halim and Hafez [38], Tang and Hafez [39]), Hafez and Guo [40].

To take advantage of the different scales involved, one may solve the viscous and inviscid flow problems separately, hence a coupling procedure is needed. Two possibilities will be discussed.

In the first method, the viscous flow calculations provide фу as boundary condition for the inviscid flow calculations, while the inviscid flow calculations provide in return фі and (фп)i for the viscous flow calculations, as shown in Fig. 9.11.

Again, the size of the overlap region must be determined based on the accuracy of the results and the convergence of iterations.

far field

flow

direction

solid body

Fig. 9.11 Sketch for method 1

In the second method, a coupling formula is introduced along the interface. The only requirement for the coupling formula is to be consistent (i. e. it does not upset the converged solution), see for example Carter’s formula [25] or semi-inverse incom­pressible flow example used by Cebeci [28] for transonic flow calculations. It is argued, however, a “better” coupling formula can be introduced if the flow physics is taken into consideration.

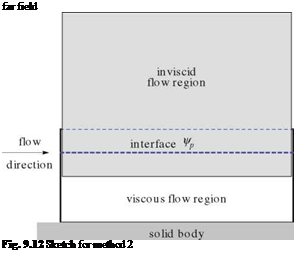An application to our simple problem is shown in Fig. 9.12.

According to Carter, a coupling formula for a semi-inverse implicit procedure could be

ФП+1 = ФПp + a(ui – uv) (9.88)

where ui is the velocity component calculated from the inviscid flow region and uv is the velocity component calculated from the viscous flow region.

In the above formula, a is a free parameter. However, since the interface must lie in a region where both the viscous and inviscid flow equations are valid, one can choose the coupling formula as follows

The first term on the right-hand-side is evaluated at level n + 1, leading to an implicit formula for фі, p and requires a tridiagonal solver.

In general, the interface equation may be the governing equation for ф, hence the coupling formula may be given for low speed flow, by

where 5ф is the correction, M is the local Mach number and p is the artificial density. Notice a should be zero for supersonic flow regions, according to the Fourier analysis!

In the above method, the overlap region consists of only three horizontal lines. The updated values of Ф p is used for both the inviscid and viscous flow regions. The latter requires also фі_p+1 to calculate ui = (фі_p+1 – фі, p)/Ay.

In general, methods with larger overlap region have better convergence. In the fol­lowing, methods using all the viscous region as an overlap region will be considered and their merits will be discussed.

Consider the same simple problem with the following splitting, method 3, Fig.9.13:

In this method, the streamfunction equation is solved in the whole domain, assum­ing w is known (in the viscous layer) and using only the no penetration boundary

Fig. 9.13 Sketch for method 3

condition on the solid surface (ф = const). The no slip condition, фп = 0, is not imposed on this step of the calculations. The viscous flow is solved as usual with the two interface conditions and the no slip and no penetration conditions at the solid surface. The vorticity calculated, in the viscous flow region, is used as a forcing function distributed over part of the domain for the first calculations. The overlap region, now, is the whole viscous flow region. Moreover, the forcing function, ш, is distributed over the whole viscous flow region. An example of this method is given in [39] for the trailing edge flow and good comparison with the full Navier-Stokes equations and triple deck theory calculations is shown.

The same example is solved in [41], using potential formulation augmented with velocity correction in the viscous layer. The governing equations are

дф

u= + u+U

д x

дф

dy

The continuity equation becomes

д2ф д2ф ди

дх2 + ду2 дх

In the momentum equation

ди ди и + v дх ду

the pressure term is approximated via linearized Bernoulli’s law, p = p0 – pUи. Notice, и = фх varies with у inside the viscous flow region. This formulation is similar to Cousteix’ recent analysis [23].

The augmented potential equation is solved everywhere with the forcing function – их, distributed in the viscous layer. Only the no penetration фп = 0 boundary condition at the solid surface is imposed. The momentum equation is solved for и with the pressure gradient given in terms of фх as a forcing function and the no slip boundary condition at the solid surface and и = фх + U at the interface (i. e. и = 0 there).

A more general formulation is adopted in [41] for the simulation of viscous flow over a rotating cylinder, where

дф и = + и + U дх	(9.95)
дф v = + v ду	(9.96)

Both the x – and the у-momentum equations are used to update и and v. The pressure terms are still evaluated based on Bernoulli’s law and in terms of фх and

фу.

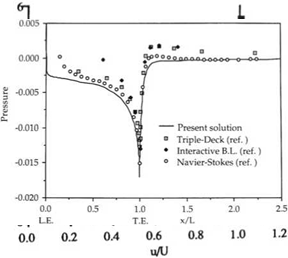
The results for finite flat plate and rotating cylinders are shown in Figs. 9.14, 9.15 and 9.16.

Finally, the approximation of the pressure in terms of фх and фу, using Bernoulli’s law can be removed. The pressure can be evaluated by integrating the normal momen­tum equation inwards, from the interface to the solid body and thus the formulation, in the viscous flow region, becomes completely equivalent to the Navier-Stokes equa­tions. This variable fidelity formulation has been used to simulate shock wave/laminar boundary layer interaction and the comparison with results of Navier-Stokes equa-

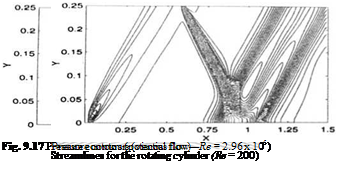Fig. 9.16

Fig. 9.18 tionsis given in Ref. [42]. Figures 9.17 and 9.18 from Ref. [42] show the wall pressure distribution and the Mach contours respectively.

The same method has been used to simulate transonic flows with shocks over airfoils and wings, see Hafez and Wahba [43-45]. It is claimed that the domain decomposition technique allows to use multigrid and upwind schemes more effl- ciently.

Viscous/inviscid interaction procedures for unsteady flows are discussed in Ref. [46, 47].

9.2 Summary of Chapter 9

Two main approaches are discussed in this chapter. The first one is based on the dis­placement thickness concept and the inviscid flow and boundary layer calculations are coupled through the displacement thickness and the streamwise pressure distri­bution. The inviscid flow and boundary layer calculations can be based on integral formulations or finite discrete approximation techniques and the four possibilities are covered. In the case where both calculations are based on integral formulations, quasi-one dimensional flow in a nozzle is studied via Pollhausen method, extended to compressible flow by Gruschwitz and by Oswatisch, as well as incompressible and supersonic flows over thin airfoils. Also, the potential flow calculation based on the streamfunction formulation, for two-dimensional flows, is coupled with the integral momentum equation. Coupling Euler calculations with boundary layer calculations are discussed in details, using several ideas.

Finally, coupling the numerical solution of the field equations of inviscid and boundary layer equations is briefly reviewed.

In the second approach, heterogeneous domain decomposition is used to cou­ple potential and Euler calculations with solutions of boundary layer or thin layer approximation of the Navier-Stokes equations. Streamfunction/vorticity formulation is described to demonstrate the concept, and potential formulation augmented with vorticity correction terms is used for compressible flow calculations.

References

1. McDevitt, J. B.: Supercritical flow about a thick circular-arc airfoil. NASA TM 78549 (1979)

2. Chattot, J.-J.: Computational Aerodynamics and Fluid Dynamics: An Introduction. Springer, New York (2002)

3. Hafez, M., Palaniswamy, S. Mariani, P.: Calculations of transonic flows with shocks using Newton’s method and direct solver. Part II. AIAA paper 88-0226 (1988)

4. Wieghardt, K.: Uber einen Energiesatz zur Brechnung Laminarer Grenzschichten. Ingen-Arch. 16, 23-243 (1948)

5. Walz, A.: Application of Wieghardt’s Energy Theorem to Velocity Profiles of One-Parameter in Laminar Boundary Layers. Rep. Aero. Res. Coun, London, No 10133. (1946)

6. Truckenbrodt, E.: An approximate method for the calculation of the laminar and turbulent boundary layer by simple quadrature for two dimensional and axially symmetric flow. JAS 19, 428-429 (1952)

7. Tani, I.: On the approximate solution of the laminar boundary layer equations. JAS 21,487-495 (1954)

8. Holt, M.: Numerical Methods in Fluid Dynamics. Springer, New York (1984)

9. Schlichting, H.: Boundary Layer Theory. McGraw Hill, New York (1979)

10. Rosenhead, L. (ed.): Laminar Boundary Layers. Oxford University Press, Oxford (1963)

11. Swafford, T., Huddleston, D., Busby, J., Chesser, B. L.: Computation of Steady and Unsteady Quasi-One-Dimensional Viscous/Inviscid Interacting Internal Flows at Subsonic. Transonic and Supersonic Mach Numbers. Final Report NASA Lewis Research Center (1992)

12. Stewartson, K.: The Theory of Laminar Boundary Layers in Compressible Fluids. Oxford University Press, Oxford (1964)

13. Gruschwitz, E.: Calcul Approche delaCouche Limite Laminaire en Ecoulement Compressible sur une Paroi Non-Conductrice de la Chaleur, ONERA, Publication No. 47 (1950)

14. Oswatitsch, K.: Gas Dynamics. Academic Press, New York (1956)

15. Liepmann, H., Roshko, A.: Elements of Gas Dynamics. Wiley, New York (1957)

16. Whitfield, D., Swafford, T., Jackocks, J.: Calculations of turbulent boundary layers with sepa­ration and viscous-inviscid interaction. AIAA J. 19(10), 1315 (1981)

17. Moses, H., Jones, R., O’Brien, W.: Simultaneous solution of the boundary layer and freestream with separated flow. AIAA J. 16(1), 419-426 (1978)

18. Le Balleur, J.-Cl.: Numerical flow calculation and viscous-inviscid interaction techniques, (1978)

19. Johnston, W., Sockol, P.: Matching procedure for viscous-inviscid interactive computations. AIAA J. 17(6), 661-665 (1979)

20. Murman, E., Bussing, T.: On the coupling of boundary-layer and Euler equations. Numerical and Physical Aspects of Aerodynamic Flows II., Springer, New York (1984)

21. Whitfield, D., Thomas, J. L.: Viscous-inviscid interaction using euler and inverse boundary – layer equations. Computational Methods in Viscous Flows. Pineridge Press, Swansea, (1984)

22. Wigton, L., Yoshihara, H.: Viscous-inviscid interaction with a three-dimensional inverse bound­ary layer code. Numerical and Physical Aspects of Aerodynamics. Springer (1984)

23. Cousteix, J., Mauss, J.: Asymptotic Analysis and Boundary Layer. Springer, New York (2007)

24. Catherall, D., Mangler, K. W.: The integration of the two-dimensional laminar boundary-layer equations past a point of vanishing skin friction. J. Fluid Mech. 26, 163-182 (1966)

25. Carter, J.: A new boundary-layer inviscid iteration technique for separated flow. AIAA paper 79-1450 (1979)

26. Brune, G. W., Rubbert, P., Nark, T.: A new approach to inviscid flow/boundary layer matching. AIAA paper 74-601 (1974)

27. Veldman, A.: New, quasi-simultaneous method to calculate interactive boundary layer. AIAA J. 19(1), 79-85 (1981)

28. Cebeci, T.: An Engineering Approach in Calculations of Aerodynamic Flows. Springer, New York (1999)

29. Wigton, L. and Holt, M.: Viscous-inviscid interaction in transonic flow. AIAA paper 81-1003 (1981)

30. Lock, R. C., Williams, B. R.: Viscous-inviscid interactions in external aerodynamics. Prog. Aerosp. Sci. 24(2), 51-171 (1987)

31. Stewartson, K.: Multistructured boundary layers on flat plates and related bodies. Adv. Appl. Mech. 14, 145-239 (1974)

32. Reynher, T., Flugge-Lotz, I.: The interaction of a shock wave with a laminar boundary layer. Int. J. Nonlinear Mech. 3(2), 173-199 (1968)

33. Drela, M., Giles, M. D.: Viscous-inviscid analysis of transonic and low Reynolds number air­foils. AIAA J. 25(10), 1347-1355 (1987)

34. Neiland, V.: Flow behind the boundary layer separation point in a supersonic stream. Fluid Dyn. 6, 378-384 (1971)

35. Sychev, V.: On laminar separation. Fluid Dyn. 7, 407-417 (1972)

36. Ryzhov, O.: Nonlinear Stability and Transition, to be Published by World Scientific. (2014)

37. Quarteroni, A., Valli, A.: Domain Decomposition Methods for Partial Differential Equations. Oxford University Press, Oxford (1999)

38. Halim, A., Hafez, M.: Calculation of Separation Bubbles using Boundary-layer Type Equations. Computational Methods in Viscous Flows. Pineridge Press, Swansea (1984)

39. Tang, C., Hafez, M.: Numerical simulation of steady compressible flows using zonal formula­tion. Part I Part II, Comput. Fluids 7-8, 989-1001 (2001)

40. Hafez, M. and Guo, W.: Simulation of steady compressible flows based on Cauchy/Riemann equations and Crocco’s relations. Part I and Part II, Int. J. Numer. Methods Fluids, 25, 1-12 and, 26, 325-344 (1998)

41. Hafez, M., Wahaba, E.: Incompressible viscous steady flow over finite plate and rotating cylin­der with suction. Comput. Fluid Dyn. J. 13(3), 571-584 (2004)

42. Hafez, M., Wahaba, E.: Hierarchical formulations for transonic flow simulations. Comput. Fluid Dyn. J. 11(4), 377-382 (2003)

43. Hafez, M., Wahaba, E.: Numerical simulations of transonic aerodynamic flows based on hier­archical formulation. Int. J. Numer. Methods Fluids, 47(6-7), 491-516 (2005)

44. Hafez, M., Wahaba, E.: Simulations of viscous transonic flows over lifting airfoils and wings. Comput. Fluids 36(1), 32-52 (2006)

45. Hafez, M., Wahaba, E.: Viscous/inviscid interaction procedures for compressible aerodynamic flow simulations. Comput. Fluids 35(7), 755-761 (2006)

46. Shatalov, A., Nakajima, M., Hafez, M.: Simulation of unsteady incompressible flows using Helmoltz-velocity decomposition. Comput. Fluid Dyn. J. 14(3), 246-254 (2005)

47. Shatalov, A., Nakajima, M., Hafez, M.: Numerical simulations of unsteady laminar incom­pressible flows using viscous/inviscid interaction procedures. Comput. Fluid Dyn. J. 15(3), 246-254 (2005)