Von Karman Integral Momentum Equation

Consider first the flat plate and incompressible flow (no pressure gradient)

The conservation theorems applied to the control volume defined in Fig.8.8 give the

8.3.1 Flow at the Trailing Edge

For potential flow around a flat plate, the surface pressure distribution is given by

(8.152)

hence, we expect the boundary layer response to this adverse pressure gradient near the trailing edge to result possibly in separation, since the pressure gradient is a forcing function in the momentum equation.

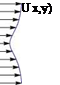
Even for a flat plate at zero angle of attack and ignoring the pressure gradient of the outer inviscid flow, at the trailing edge the skin friction is discontinuous as shown in Fig. 8.11.

The displacement thickness will have discontinuity in the derivative at the trailing edge. The inviscid pressure over the augmented body will not be regular in x.

More sophisticated treatment is required to account for separation, trailing edge singularity and curvature of the wake.

Fig. 8.11 Boundary layer in the vicinity of the trailing edge