Wedge flows

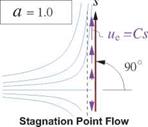
The Falkner-Skan solutions are strictly valid only for flows with the power-law edge velocity distribution. It is fortuitous that such potential flows do indeed occur over simple geometries, the so-called wedge flows. Three particular wedge flows are shown in Figure 4.13, and their boundary layer solution parameters are also listed in Table 4.1. The case of a = 1, called stagnation point flow, occurs in practically every aerodynamic flow which has a body with a blunt leading edge, such as a common airfoil. For this flow we have 6FS = ■Jv/C, so that the boundary layer thickness near a stagnation point is locally constant.

Figure 4.13: Three particular wedge flows. Displacement effect not shown.

The case a = 0, corresponding to a constant pressure and edge velocity, is commonly called flat plate flow or Blasius flow. For this case we have <SPS = fvsjC, so that the boundary layer thickness grows as л/s. A Blasius boundary layer is commonly used as a first approximation to laminar boundary layer flows which have nearly-constant pressure or edge velocity over most of their extent.

The last case a = -0.0904 shown in Figure 4.13 is called incipient separation flow, which has zero skin friction everywhere. This wedge flow is mainly a mathematical curiosity, since the top and bottom flows occupy the same space above the plate which is physically impossible. A more plausible example is a thin airfoil whose camber shape is such that it has the ue(s) ~ s-0 0904 edge velocity distribution on one side. However, since the incipient-separation boundary layer is theoretically infinitely sensitive to any ue(s)
perturbations and hence to geometric irregularities, such an airfoil flow would still be virtually impossible to realize in practice. Incipient separation flow is also very susceptible to transition to turbulent flow, as will be discussed in Section 4.14, and therefore can exist only at relatively low Reynolds numbers. In this case it will have large viscous displacement effects, which will further complicate the realization of such a flow.

Besides providing physical insight and quantitative results for the special case of wedge power-law flows, the Falkner Skan solutions are also very useful for “calibrating” approximate integral solution methods for general boundary layer flows. These will be treated in Section 4.11.