Weissinger’s L-Method
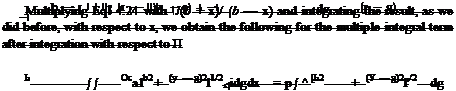
The Prandtl’s lifting line theory is not valid for the wings which have forward of backward sweep of more than 15°. For highly swept wings the method proposed by Weissenger is widely used. Weissenger’s method, rather than ignoring the terms with (x — П), it replaces by half chord, b, to simplify Eq. 4.11a. This approximation is justified physically because it considers the average value of term (x — П) rather than neglecting it. Rewriting Eq. 4.11a with this simplification we obtain
This alteration saves the second term on the right hand side of 4.28 being from singular. Now, we define the Weissenger’s L function
In this form Eq. 4.29 is valid for the wings with their quarter chord line parallel
to y axis
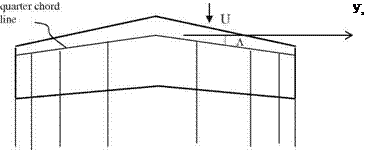 |
When the wing has a sweep, Weissinger places the bound vortex at the quarter chord line and applies the boundary conditions at the three quarter chord line. The bound vortex is placed at both sides of the wing with the sweep angle Л as shown in figure below where the wake vortices are also indicated as straight lines parallel to main stream
Let us now write down the Weissenger’s L(y, g ) function with sweep
![]()
![]() 11 1 dG dg* l* dG
11 1 dG dg* l* dG
The L function in 4.30 is more complex compared to the one in 4.29, (BAH 1996). For y > 0 ve g > 0 the function becomes
(4.31)
When sweep angle Л goes to zero, Eq. 4.31 becomes 4.29. If we transform the spanwise coordinates, as we did for the case of lifting line theory with y* = cosu and g* = cosh and expand the circulation term into Fourier sin series, the necessary aerodynamic coefficients are obtained through solution of 4.30 (BAH 1996).










