. Canonical supersonic flow

The PG transformation (8.65), (8.66) can be applied to the supersonic case if the redefined в is used. Now the PG equation (8.60) reduces to

— фхх + фуу + <f>zz — 0 (8.142)

which is the wave equation. It has an implied M00 = y/2,p = l, so that its characteristics have slopes of ±1. This is called the canonical supersonic flow. This is only a minor simplification from the physical flow, since it does not provide any special advantages for solving supersonic flow problems, unlike in subsonic flow where the canonical flow is incompressible. Here its main advantage is theoretical, in that the properties of all small-disturbance supersonic flows can be investigated by considering only the canonical case.

8.8.3 Supersonic singularities

The linearity of the PG equation allows the construction of general 3D flows by superposition of supersonic singularities. These are analogues of the subsonic source, vortex, and doublet singularities, but have a num­ber of important differences. One major difference is that a supersonic singularity is singular everywhere on its Mach cone surface, not just at a single point like in the subsonic case, and is also undefined in some regions of space. These features will require care in the construction of supersonic superposition integrals.

Hyperbolic radius

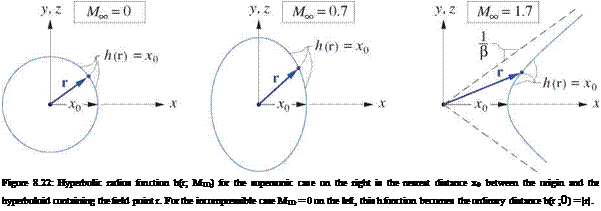
For defining supersonic-singularity kernel functions, a useful field function is the hyperbolic radius,

/Hr;Moo) = л/х2 -{Ml-l){y2+z2) (8.143)

which is the closest distance between the singularity point at the origin and the hyperboloid surface contain­ing the field point r, as shown in Figure 8.22. The term “radius” originates from the observation that for the incompressible case M =0 it reduces to the actual distance function h{r;0) = |r| = Jx2 y2 z2. For a singularity point located at some arbitrary location r’ other than the origin, the hyperbolic radius is obtained by the usual shift of the function’s argument, h(r-r’; ). The equation

h(r-r’; MTO) — 0

therefore defines a Mach cone with its apex at location r’.

Supersonic point source

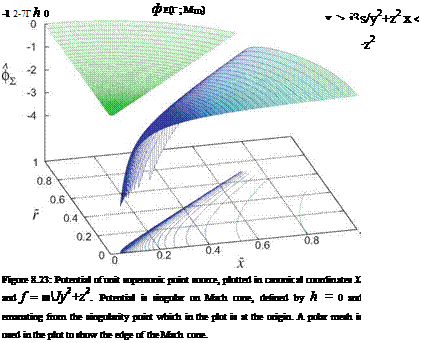
The basic 3D singularity from which all others can be constructed is the supersonic point source, which has the following unit-strength potential or kernel function, plotted in Figure 8.23.

The term “source” is a bit misleading here, since this flow-field is not just the usual point source at the origin, but also includes the field source distribution

which is generated by the point source. It’s also important to note that an isolated supersonic source of finite strength is not physical, since its a field has an infinite strength everywhere on its h(r) = 0 Mach cone
surface. The velocity field also has a very strong 1/|r — r’j2 singularity everywhere in the vicinity of the Mach cone surface. A more physical flow-field will be obtained only after a distribution of infinitesimal point sources is superimposed, as will be considered in the following sections.

Supersonic line source

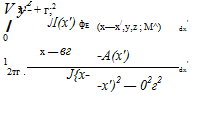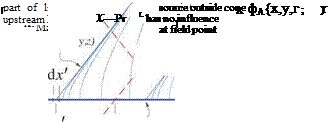
Superposition of a line of supersonic point sources (8.144) along the x-axis, from the origin downstream, creates a supersonic line source. This can represent supersonic flow over a body of revolution.

The radial distance r from the x-axis will be convenient to use for axisymmetric potential distributions such as this one. Note that this is a change in notation from elsewhere in this book, where r typically denotes jrj.

The integration range in (8.145) is restricted to only those point sources on the x-axis which can influence the field point x, y, z. This range is what lies inside the upstream Mach cone emanating from the field point, as sketched in the figure above.

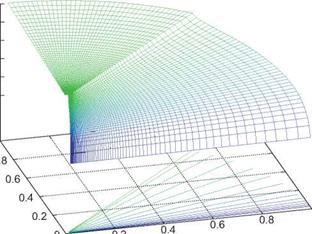
For the case of a unit line-source density Л(х) = 1, we can integrate (8.145) to give the unit line source potential, shown plotted in Figure 8.24.

Note that the highly singular nature of the point source potential has been mitigated to a weak logarithmic singularity for the line source. The strength of the perturbation velocities дфA/дx and дфA/дr, has also been mitigated to a 1/|r — r’j singularity along the origin’s Mach cone where h = 0, and also on the x-axis where r = 0.

The local source line strength Л(х) required to model a body of revolution with area and corresponding radius distributions А(х) = пЯ(х)2 can be determined by same approach used in the subsonic case. Remembering that ф is normalized with the freestream velocity, the flow tangency condition at the body surface is

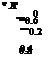1

Figure 8.24: Potential of a unit supersonic line source extending from the origin downstream.

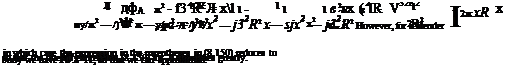which when rewritten using the unit-strength radial velocity (8.149) gives the required line source strength Л in terms of the body geometry.

A 1

. ndR dA

Л = ‘2ttR-— = — dx dx

Aside from a factor of (Л here corresponds to Л/V^ as defined previously), the line source strength (8.151)

is exactly the same as expression (6.72) for a slender body in incompressible flow. Since Л here also depends only on the total cross-sectional area A(x), it can be used for bodies which aren’t exactly axisymmetric.