CONFORMAL MAPPING AND THE JOUKOWSKI TRANSFORMATION

The method of solution for our model airfoil problem is to map the airfoil (which is in the physical plane Y = x + iz) to a circular cylinder in the / = g + ih plane through the conformal mapping Y = Y(f). The solution in the circle plane has already been obtained (in Section 3.11). Let the complex potential in the circle plane be F(f) and the complex velocity W(f). Then the results in the physical plane are

F(Y) = F[f(Y)] dF dF df 1

w^dY=^d=w(f^f

The complex velocity in the physical plane is given as a function of the transformation variable f. The following three model problems are all special cases of the Joukowski transformation

C2

r‘f+w

where C will be shown to be the chord for a flat plate, circular arc, and approximately for a symmetrical foil.

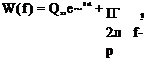Consider the mapping from the airfoil to the circle shown in Fig. 6.9. The complex velocity at infinity in both planes is Q^e ‘a and the transformation has two free parameters, the radius of the circle a and the center of the circle p. The complex velocity in the circle plane is obtained with the aid of the results of the flow over a cylinder from Section 3.11:

Since the airfoil has a sharp trailing edge and the circle has no corners, the transformation must have a critical point (dY/df = 0) at the point in the circle plane corresponding to the airfoil trailing edge. Denote this point by fe- The Kutta condition requires the velocity at the airfoil trailing edge to be finite

FIGURE 6.9 Joukowski transformation: mapping of airfoil to circle.

and therefore from Eq. (6.23) it can only be satisfied if

W(/„) = 0 (6.26)

In the circle plane fK = C/4 and the coordinate system is shown in Fig. 6.9. (Note that / = – C/4 is also a critical point and must be placed inside the circle to avoid a velocity singularity in the flowfield. The critical points f = ±C/4 transform to Y = ±C/2.) From the figure, it is seen that

fe-ti = ае~ф (6.27)

If this is substituted into Eq. (6.25) for W(f) and the Kutta condition is applied, we get

Q„e-ia + e* – Q-eiae2ip = 0

2 ла

-2jtaQJe~*a+l>) + Г + 2naQJeKa+p) = 0 and the circulation is

Г = 4ла(2«> sin (a + /3) (6.28)

The lift and lift coefficient are then given by

L = pQooT (6-29)

С, = т—^Г = 8л:-sin (a + (6.29 a)

pQlc c

Let the surface of the circle be given by

f = p + ae, e (6.30)

as shown in Fig. 6.9. The complex velocity on the circle is then obtained by

substituting Eqs. (6.28) and (6.30) into Eq. (6.25):

W(f) = Q„e~la + 2sin (a + р)е~ів – <2„е-іае~ш = Q„e-,e[e"'(e,“e) + 2/ sin (a + /3) – eKa~e)]

= 2j’6»(sin (or + /3) – sin (a — 0)]e_,e (6.31)

and the complex velocity on the airfoil surface is obtained from Eq. (6.23).

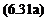
W(/)

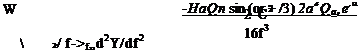To find the complex velocity at the airfoil trailing edge, L’Hospital’s Rule must be applied since both W(f) and dY/df are zero there. At the trailing edge / = C/4 and в = 2л – /3 and the complex velocity is found to be

Using ft-p = aew, we get

= 2*"®[—і sin (a + /3) + e'(“ e)] = Qx,^e2ipcos (a + fi)

(6.32)