DEPENDENCE ON h

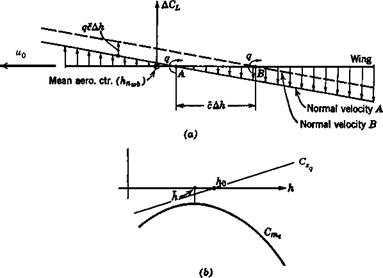
Because the axis of rotation in Fig. 5.5, passes through the CG, the results obtained are dependent on h. The nature of this variation is found as follows. Let the axis of rotation be at A in Fig. 5.6, and let the associated lift and moment be

CLa = CLqAq CmA — C^q (5.4,7)

Now let the axis of rotation be moved to B, with the change in normal velocity distri­bution shown on the figure. Since the two normal velocity distributions differ by a constant, (the upward translation qc Ah) the difference between the two pressure dis­tributions is that associated with a flat plate at angle of attack

a = — —— Ah (5.4,8)

u0

This angle of attack introduces a lift increment acting at the wing mean aerodynamic center of amount

ACL = CLa= AhCL = -2CL q Ah

“ «о “

Figure 5.6 Effect of CG location on CZq, Cm.

We see that CLq is linear in h, and can therefore be expressed as

CLq = ~2CLa(h – ho) (5.4,11)

where h0 is the CG location at which CZq is zero. By virtue of (5.1,1) we get

CZq = ~CLq = 2CLa(h – h0) (5.4,12)

The pitching moment about the CG is

Cm = Cmac + CL(h – hnJ (5.4,13)

so that Cmq=-^ + CLq(h-h„J

= – 2CLa(h – h0)(h – hj (5.4,14)

Equation (5.4,14) shows that Cmq is quadratic in h. We can write it without loss of generality as

Cmq = Cmq – 2ClJJi – h)2 (5.4,15)

where Cmq is the maximum (least negative) value of Cmq and h is the CG location where it occurs (see Fig. 5.6b). The value of h is found by differentiating (5.4,14). This yields

The linear theory of two-dimensional thin wings gives for supersonic flow:

h0 = h =

and for subsonic flow:

h0 4

h = I (5.4,18)