Discretization

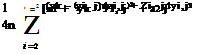The discrete formulation is now described. The influence coefficients are calculated as

with the notation introduced earlier and in Fig. 10.10. The contributions to aj, k and Cjk of the vortex filament part that is beyond the Trefftz plane are approximated by the following remainders

(10.64)

The torque and thrust coefficients are discretized as

jx 1

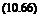Ct = Гк (1 + Uk) yk (Пк – Пк-1)

ТҐ

Each contributes to the minimization equation

д Ct 2 . .

щ = п + uj)yj (пj – пj-1)

jx-1

+ п^Гк^-1, к – aj, к + aj, k)Уk (Пк – Пк-1), j = 2 ,jx – 1 (10.68) д С т 2 y j

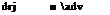—————- (о* + “’j)(пj- пj-1)

jx 1

п^Гк c-1,к – Cj, к) (пк – Пк-1), j = 2,…, jx – 1 (10.69)

Boundary conditions complete the formulation with Г1 = rjx = 0 The minimization equation

is a linear, non-homogeneous system for the rj’s that can be solved by relaxation. Let Arj = Г”+1 – Г" be the change of circulation between iterations n and iteration n + 1, and ш the relaxation factor. The iterative process reads

_(i +uj)yj – X( adv + w j)]

jx 1

^ rk {(pj-1,k – aj, k + aj, k) yk – A (cj-1,k – cj,^] (Лк – Vk-1) (10.71)

k=2

With Jx = 101 and ш = 1.8 the solution converges in a few hundreds iterations. Note that if X = adv the system is homogeneous and the solution is rj = 0, Vj, which corresponds to zero loading of the rotor that rotates freely and does not disturb the flow. This is called “freewheeling”. For a given X the solution corresponds to a certain thrust. In order to find the value of the Lagrange multiplier that will correspond to the desired value of the thrust coefficient, say CTtarget, CT and CT are decomposed into linear and bilinear forms in terms of the rj’s

jx-1 jx-1

22

CT = CT1 + Ст2 = – X rjyj(nj-nj-1) + – x rJuJyj(nj – nj-1) (1°.72)

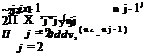j =2

(10.73)

CT1 and CT1 are homogeneous of degree one. CT2 and CT2 are homogeneous of degree two. Using the properties of homogeneous forms, the summation of the min­imization equations multiplied each by the corresponding rj results in the identity

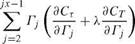Ct 1 + 2Cr2 + X (Ct 1 + 2Ct2)

jx-1

= Г {(1 + 2uj)yj – x(Ov + 2wj)} (nj – nj-1) = 0 (10.74)

j =2

which is the discrete analog of the optimum condition derived earlier.

If one assumes that the optimum distributions of circulation for different CTtarget vary approximately by a multiplication factor, then knowing the solution rj for a particular value of X (say X = 0) allows to find a new value of the Lagrange multiplier as follows. Change the rj’s to new values k^. In order to satisfy the constraint one must have

Ct target = К Ct 1 + К 2Ct2 (10.75)

Solving for к yields

The new estimate for X is obtained from the above identity as

CT1 + 2k CT 2

Ct 1 + 2k Ct 2

This procedure is repeated two or three times to produce the desired solution. Once the optimum circulation is obtained, the chord distribution is given by

where (Ci(a))opt corresponds to the point a on the polar such that Ci/Cd is maxi­mum. The twist distribution results from

tj = ф j a