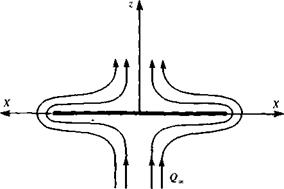
Flow Normal to a Flat Plate

Another interesting solution that can be obtained by this method is the solution for the flow normal to a flat plate. The complex potential for this flow in the circle plane is obtained by adding the potentials of a stream in the z direction and an opposing doublet (the flow is symmetric about midchord and has zero circulation) and is given by

(6.47)

On the surface of the circle / = (с/4)e, e and the complex potential becomes

The complex potential on the surface is seen to be real and therefore it is equal to the velocity potential. The jump in potential across the plate is therefore given by

ДФ = QccVl – {2x! c f

Both an application of the Kutta-Joukowski theorem and a pressure integration yield the result that there is no force acting on the plate (recall that this is a potential flow solution without any flow separations!). Based on the results of the previous section, however, it is expected that symmetrically placed tip forces may be acting on the tips of the plate and these will be important in the slender-wing application.

Consider the flow in the neighborhood of the left tip where / is approximately — c/4. The complex velocity at the corresponding point on the circle is obtained by a differentiation of the complex potential (Eq. (6.47)) as

W(f) = -2iQ

The analysis now proceeds in an identical fashion to the analysis in the previous section since the transformation is the same and the complex velocity in the neighborhood of the tip is

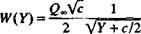(6.51)

The tip force is then calculated and is

npcQl

The force acts to the left and from symmetry a tip force of equal magnitude acts on the right tip and points to the right (see Fig. 6.13).