Force and Moment Coefficients

L 2 pV 2S

D 2 pV 2S

The important aerodynamic forces and moment associated with a flying machine, such as an aircraft, are the lift L, the drag D, and the pitching moment M. The lift and drag forces can be expressed as dimensionless numbers, popularly known as lift coefficient CL and drag coefficient CD, by dividing L and D with 2pV2S. Thus:

pV2 Sc

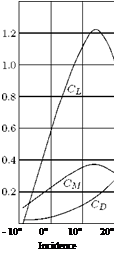
The variation of CL and CD with the geometrical incidence a is shown in Figure 1.13. The pitching moment, which is the moment of the aerodynamic force about an axis perpendicular to the plane of symmetry (about y-axis in Figure 1.3), will depend on the particular axis chosen. Denoting the pitching moment about the chosen axis by M (note that M is also used for denoting Mach number, which is the ratio of local flow speed and local speed of sound), we define the pitching moment coefficient as:

where c is the chord of the wing. A typical variations of CL, CD and CM with angle of attack a are shown in Figure 1.13.

Note that the aerodynamic coefficients CL, the drag CD and the moment CM are dimensionless parameters.

Figure 1.13 Variation of lift, drag and pitching moment coefficients with geometrical incidence.

Example 1.4

An aircraft weighing 20 kN is in level flight at an altitude where the pressure and temperature are 45 kPa and 0 °C, respectively. If the flight speed is 400 km/h and the span and mean chord of the wings are 10 m and 1.5 m, determine the lift coefficient.

Solution

Given, W = 20, 000 N, 2b = 10 m, c = 1.5 m, V = 400/3.6 = 111.11 m/s, p = 45 kPa, T = 0 + 273.15 = 273.15 K.

The density of air is:

p

RT

45, 000

= 287 x 273.15 = 0.574 kg/m3.

The planform area of the wing is:

S = 2b x c = 10 x 1.5 = 15m2.

In level flight, the weight of the aircraft is equal to the lift. Thus:

L = 20, 000 N.

Therefore, by Equation (1.4a), the lift coefficient becomes:

L

2 pV 2S

20, 000

2 x 0.574 x 11 1.11 2 x 1 5