. Infinite swept wing Swept-wing potential flow

An infinite swept cylindrical body, such as a wing for example, is shown in Figure 4.19. The perpendicular and parallel freestream velocity components are

V± = VTO cos Л V = VTO si^

where Л is the sweep angle. The x, z surface coordinates are chosen such that z runs spanwise, with x being the usual 2D-like chordwise coordinate.

Since there is no special z location on the wing, we must have

^>=0

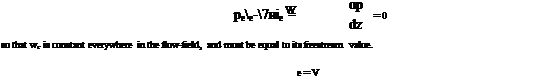for all flow quantities. In the potential flow, the z-momentum equation which governs we then simplifies to

PeO = Pc* ( y~

The local pressure is given by the isentropic relation (1.112), or by the Bernoulli equation (1.112) for the case of low speed flow.

In either case, the spanwise velocity we has no influence on the pressure, and hence no influence on the lift. It is therefore appropriate and useful to define “perpendicular” pressure and lift coefficients referenced to the perpendicular dynamic pressure,

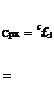Pe-Pco pooV’l

where ACp± is the pressure coefficient difference between the lower and upper surface of the airfoil, and cL is the perpendicular chord. These quantities correspond to those of a 2D flow in which the spanwise velocity V is absent. So for example, CP± (x ; ) and в£± («x ) on a high aspect ratio swept wing can be obtained from

2D calculations or 2D experimental data, with

fyert

a± = arcsm ——

Vl

being the angle of attack seen in the perpendicular plane, and VVert is net vertical freestream velocity reduced by the local 3D induced downwash velocity.

Swept-wing boundary layer flow

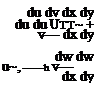With the d()/dz = 0 condition, the 3D boundary layer equations for low speed flow, with the kinematic eddy viscosity vt = pt/p invoked, simplify as follows.

Evidently (4.77) and (4.78) are the 2D boundary layer equations in x, y, decoupled from the z-momentum equation (4.79) and the spanwise w velocity. As pointed out in the previous section, ue(x) and the pressure are the same as in a 2D flow with we absent. Hence, the chordwise velocities u, v governed by (4.77),(4.78) are also the same as in 2D flow, and are unaffected by the spanwise flow component.

Because neither the local potential flow nor the boundary layer flow are affected by the V spanwise veloc­ity component, the overall conclusion is that the relevant airfoil shape which determines the aerodynamic characteristics of a swept high aspect ratio wing is perpendicular to the wing, not parallel to the freestream direction. In particular, adding a spanwise freestream velocity component to a given wing does not affect its surface pressures and lift, and also does not affect its boundary layer its separation resistance or chordwise separation location for the same perpendicular-plane angle of attack. This is shown in Figure 4.20.

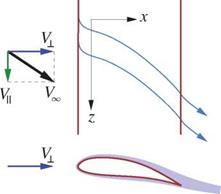Figure 4.20: Adding a spanwise freestream velocity component V does not affect a wing’s lift, or the characteristics of a laminar boundary layer projected onto the perpendicular plane. A turbulent boundary layer will change somewhat from the larger Reynolds number’s effect on the turbulence.

The independence of the chordwise u(x, y) velocity from the spanwise w(x, y) velocity is strictly valid only for laminar flow. For turbulent flow, the spanwise velocity will increase the effective Reynolds number of the turbulence, and hence will have some effect on vt, so the decoupling isn’t perfect. Nevertheless, since Reynolds number effects on turbulence are weak, the conclusions are very nearly correct also for turbulent flow. McLean [18] discusses the effects of wing sweep on boundary layers in much more detail.