Leading-Edge Suction

In the previous section the force on a flat plate airfoil is obtained with the use of the Kutta-Joukowski Theorem and is seen to be perpendicular to the free stream direction. An apparent problem arises if we attempt to find the force by an integration of the pressure distribution. On the surface of the plate the velocity is given in Eq. (6.35) and with the use of the Bernoulli equation the pressure difference across the plate is given as

V

I — ‘2jX/c

1 + 2x/c (6.38)

The force Z is perpendicular to the plate and is obtained by integrating the pressure difference along the plate to get

The force obtained by these two different approaches is not the same in either magnitude or direction.

The difference can be explained by considering the flat plate as the limiting case of a thin airfoil as its thickness goes to zero. In this limit the pressure at the leading edge increases while the area upon which it acts decreases until in the flat plate limit the pressure is infinite and the area is zero. In this limit there is a finite contribution to the force that must be added to the result obtained by the pressure integration. To obtain this force we surround the plate leading edge by a small circle and calculate the force with the use of the Blasius formula.

The complex velocity on the plate is given in Eqs. (6.31) and (6.31a). The velocity on the circle at the leading edge is obtained by using Eq. (6.31) with /3 = 0 and в = л and is

W(f) = —4iQx sin a (6.40)

Near the leading edge / is approximately —c/4 and therefore we can take

If the transformation in Eq. (6.24) is now inverted and У is set approximately equal to — c/2, the transformation becomes

f = h{Y + УУ2-с2/4) = – C – + iifcyjY + d2 (6.42)

the leading-edge region is therefore seen to be (from

e^y^sinnr

ЩУ) VT + c/2

This velocity is now substituted into the Blasius formula (Eq. (6.19)) to get

X – iZ = y J W2dY = Y Qlc sin2 or J = ~прс0& s*n2 01 (6-44)

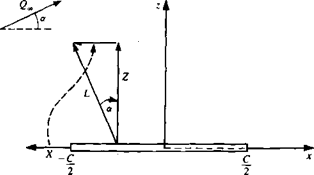
This leading edge force is seen to act along the plate in the upstream direction (Fig. 6.12) and is called the leading-edge suction force.

The total force is now obtained by the addition of the pressure force and the suction force (Eqs. (6.39) and (6.44)) and the resultant force is seen to be perpendicular to the stream and exactly equal to the result from the Kutta-Joukowski theorem (see Fig. 6.12).

A generalization of these results can be applied to the solution of the small-disturbance version of the thin-airfoil problem. Assume that this solution has the following complex velocity in the neighborhood of the airfoil leading edge,

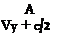
W(Y) =

FIGURE 6.12

Forces due to pressure difference and leading edge suction on the flat plate at angle of attack. Note that the resultant force (lift) is normal to the free stream Q^.

where A is a constant. Then the leading-edge suction force in this situation is given by the Blasius formula as

X = —JtpA2