Low Aspect Ratio Wings

Prandtl’s theory works for high aspect ratio wings and Weissinger’s theory works for wings with medium aspect ratios. Jones’ theory, on the other hand, is applicable to the wings having low aspect ratio. By studying Jones’ theory, we will be covering all ranges of aspect ratios for the thin wings. In low aspect ratio wings we usually study the planforms having curved leading edges as shown in Fig. 4.3.

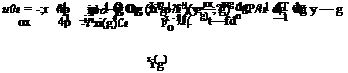Since the trailing edge is a straight line, the integral Eq. 4.11b can be inverted. This time we neglect (y — g)2 compared to (x — f)2 to obtain

Taking care of the terms with absolute value and breaking the integrals we obtain

If we write the bound vortex sheet strength in terms of the perturbation potential differences between the upper and lower surface, Аф’ = ф’и — ф’ we have

The integral in Eq. 4.33 is taken at a section from leading edge to a point x on the chord. In order to cover the full wing, the spanwise integration must be taken from ±1 to ± b(x) as shown in Fig. 4.3. Equation 4.32 becomes

b(x)

U! r=-h y—g щАф,(х-g)dg

—b(x)

Equation 4.34 can be directly inverted. Nondimensionalizing with y* = y/b(x) and g* = g/b(x) Eq. 4.34 then reads as

If we further nondimensionalize the following integral to obtain

11

OMdg.’ ^ ‘аф’ = 0.

0 g b(x) 0 g* b(x) ф

11

Using the property as f (g*) = ДгАф’ having zero integral between —1 and 1 as

follows we have

g(y*) = 2“ У ~T~:*dn* and if У f (n*)dn* = 0 then (4.37a)

Taking care of the signs and using – UOr1 for g in 4.37a, 4.37b we have

1

OA/’ = 2U f bzaJ 1 – n*2d *

Oy 1 – y*2 Ox y* – n* П

In dimensional form it becomes

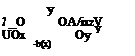The linearized form of Kelvin’s equation, 3.5 in Chap. 3, gives us the relation between the lifting pressure coefficient and the surface vortex sheet as follows

Since the integrand of 4.39 is equal to the right hand side of 4.38, for the known wing geometry the lifting pressure coefficient can be found via 4.39.

If we assume that for the low aspect ratio wings the elastic deformations and the camber exist only in the chordwise direction, i. e., OzJOy = 0, the integral in 4.39 is easily evaluated. The singular integral given below evaluates to

= “y.

If above integral is placed in 4.38 we obtain

(4.40)

Equation 4.40 provides the lifting pressure coefficient explicitly for the low aspect ratio wings. The validity of 4.40 depends on satisfying the Kutta condition at the trailing edge. The first term of 4.40 goes to zero for uncambered wings. The second term on the other hand is zero if the span remains constant at the trailing edge. Satisfying these two conditions makes the Jones’ approach applicable, otherwise it will not be applicable. Figure 4.3 has a planform shape which has a constant span at the trailing edge to satisfy the Kutta condition.

Let us find the sectional lift of a low aspect ratio wing by integrating 4.40 along the chord.

bo bo

Г’М=2 PU cr. dx =-2„U’- OX [|y b2(x)-f-

Xl Xi

=-2pU2pr-y2( I-),

The end result of 4.41 tells us that a low aspect ratio wing deformable only in chordwise direction is elliptically loaded and this load is proportional with the angle of attack at the trailing edge. The total lift now can be found by integrating 4.41 in spanwise direction.

Here, a is the angle of attack for a straight planform wing. If we write the aspect ratio as follows AR = (2i)2/S, the lift line slope for the wing becomes

Equation 4.43 is used for usually delta wings.

Now, we can also calculate the chordwise variation of lift which is usually done for the delta wings.

Jones’ approach gives small downwash values compared to the free stream speed. For low aspect ratio delta wings this means small cross flow velocity even for the high free stream speeds in compressible flows. The cross flow becoming incompressible enables us to apply Eq. 4.43 even for the case of supersonic flows.

As seen from Eq. 4.41, the spanwise load distribution is elliptic which now yields an induced drag for the low aspect ratio wings

CDi = CL/(pAR). (4.45)

Example 2: For a low aspect ratio delta wing with angle of attack a, plot the chordwise load distribution on the wing.

Solution: The equation of leading edge is given by b(x) = (x + bo)l/(2bo). Equation 4.44 gives the chordwise distribution as follows

and ci(x) = yU^bb = na|r(x + bo).

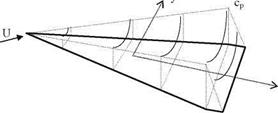
In order to satisfy the Kutta condition the trailing edge ends with a constant span as shown in Fig. 4.4.