Newton Flow

6.7.1 Basics of Newton Flow

At flight with very large speed, respective Mach number, the enthalpy hof the undisturbed atmosphere is small compared to the kinetic energy of the flow relative to the moving flight vehicle. The relation for the total enthalpy, eq. (3.2), can be reduced to

M, x – T oo : ht = (6.143)

If we neglect the flow enthalpy also in the flow field at the body surface, the forces exerted on the body would be due only to the kinetic energy of the fluid particles. A corresponding mathematical flow model was proposed by I. Newton [22]. His model assumes that the fluid particles, coming as a
parallel stream, hit the body surface, exert a force, and then move away parallel to the body surface, Fig. 6.34 a). With the notation given in that figure, we obtain for the force R* acting on an infinitely thin flat plate with the reference surface A

R* = pv2 sin2 aA. (6.144)

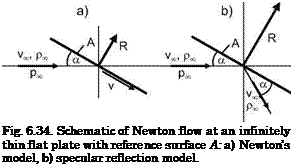This is in contrast to specular reflection, Fig. 6.34 b) (free-molecular flow), which would lead to a force twice as large. However, case a) models surpris­ingly well the actual forces in the continuum flow regime.

If we also take into account the ambient pressure pTO, we get the aerody­namic force acting on the windward side of the flat plate

R = (provj^ sin2 a + p^)A. (6.145)

The surface-pressure coefficient on the windward side, cPws, then is

On the leeward side of the flat plate only the ambient pressure acts, p = pro, because this side is not hit by the incoming free-stream.[75] The surface – pressure coefficient on this side, cPls, hence is

With the usual definitions we find the lift and the drag coefficient for the infinitely thin flat plate

CL = (cPws — cpis) cos a = 2 sin2 a cos a,

and

CD = (cPws — cpis) sin a = 2 sin3 a. (6.149)

The resulting force coefficient has the same value as the pressure coeffi­cient on the windward side:

CR = (cPws — cpis) = 2 sin2 a. (6.150)

These relations obviously are valid only for large Mach numbers. Take for instance an airfoil in subsonic flow. Its lift at angles of attack up to approximately maximum lift is directly proportional to the angle of attack a, and not to cos a sin2 a.

Newton’s model is the constitutive element of “local surface inclination” or “impact” methods for the determination of aerodynamic forces and even flow fields at large Mach numbers. In design work, especially with incremental approaches, it can be used down to flight Mach numbers as low as Ыж « 3 to 4 [38].

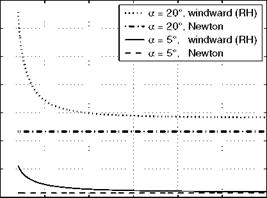
If we compare pressure coefficients at the windward side of an infinitely thin flat plate at angle of attack, the RHPM-flyer [1], we find at all angles of attack a, that the Newton value is below the exact value, Fig. 6.35, where results for two angles of attack are given. The difference increases with in­creasing a, and decreases with increasing MTO.

0.7

0

The exact (RH = Rankine Hugoniot) value obviously becomes “Mach- number independent” (Section 6.8) for Ыж ^ 8. For a sharp-nosed cone Mach-number independence is found already at Ыж ^ 4, and the Newton result lies closer to, but still below, the exact result.

Certainly there is a physical meaning behind Newton’s model. It is Mach – number independent per se, and the difference to the exact value becomes smaller with decreasing ratio of specific heats 7. We find an explanation, when we reconsider the pressure coefficient behind the oblique shock for very large Mach numbers, eq. (6.105)

, ^ 4sin2 в. _ _.

M, x -> 00 : Cp у————- —, (6.151)

Y +1

and also the relation between the shock angle в and the ramp angle S for very large Mach numbers, eq. (6.117)

Y +1

Moo —> 00 : в —> —-—S. (6.152)

For y ^ 1 we obtain that the shock surface lies on the ramp surface (infinitely thin shock layer):

в ^ S, (6.153)

and hence

cp ^ 2sin2 S. (6.154)

Since the ramp angle S is the angle of attack a of the flat plate, we have found the result, see eq. (6.146), that in the limit Мж ^ ж, and y ^ 1, Newton’s theory is exact. This is illustrated in Fig. 6.36, where with increasing Mach number and decreasing ratio of specific heats finally the exact solution meets Newton’s result.