ROBUST PERFORMANCE: SENSITIVITY FUNCTION (P3)

15 -25 ■ ft.

frequency in racVs

Figure 6.5. Missile autopilot – template for robust performance – nominal sensitivity

function in dashdot line – template of (Balas and Packard, 1992) in dashed line (with

factor 0.9) – new template in solid line.

Robust performance is analyzed in the frequency domain, using the sensitivity function S (see section 2. of chapter 2 for the definition of S). A fictitious performance block is added to the model perturbation, which now contains 4 non repeated real scalars and a full complex block.

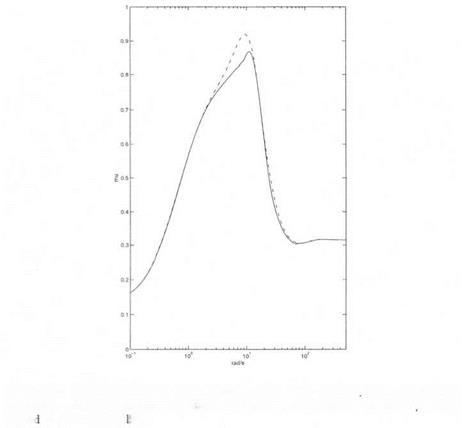
Figure 6.6. Missile autopilot – robust performance (P3) – mixed и lower and upper bounds in solid and dashed lines (the two plots nearly coincide) – complex и upper bourn in (lash-clotted ine.

The template on the sensitivity function S is essentially the same as the one in (Balas and Packard, 1992), except that the low frequency performance is relaxed and that the template is multiplied by factor 0.9 (see Figure 6.5). The low frequency performance is relaxed in order to focus on the performance at medium frequencies. On the other hand, the template is multiplied by 0.9, so as to choose the worst allowable performance as uic = 4 rad/s and tr«^ = 0.25s (the bandwidth of the nominal sensitivity function S iscuc = 5 rad/s, thus leading to a nominal closed loop rise time tr w 0.20s).

Figure 6.6 presents the mixed p lower and upper bounds in solid and dashed lines and the complex p upper bound in dash-dotted line. The mixed p lower and upper bounds nearly coincide at all frequencies. The maximal value of the mixed p upper bound is 0.87 at ui = 11.00 rad/s (the result is nearly non conservative). The corresponding uncertainty in the stability derivatives is thus 5/0.87 « 5.8%.

Note finally that a peak at medium frequency is here again obtained (around 11 rad/s). This strongly suggests that the degradation of the stability and performance properties is essentially due to a decrease of the damping ratios of some closed loop poles at medium frequencies.