Single Time Step Method: Runge-Kutta Scheme

One of the most popular time marching methods is the Runge-Kutta (RK) scheme. The RK scheme is based on Taylor series truncation. A widely used RK scheme is the fourth-order method. To illustrate the basic approach of the RK method, let the time axis be divided into increments of At. Suppose the solution of a differential equation,

£=f<">- (31)

where u and F are vectors, and time level n is known. To find the solution at the next time level (n + 1), four evaluations of the derivative function F are performed (fourth-order RK). These intermediate evaluations provide indirectly the high-order derivatives of u so that a matching of high-order terms in At in a Taylor series expansion becomes possible. The following is a very general form of the fourth- order RK scheme:

4

u(n+1) = u(n) + J2 wjКj j=1

К = F (uw) At k2 = F (uw + p2k1) At k3 = F (u(n) + e3k2) At k4 = F (u(n) + e4k3) At.

Superscript (n) indicates the time level. The constants в2, в3, в4, w1, w2, w3, and w4 are chosen so that, when the left and right sides of Eq. (3.2) are expanded in Taylor series for small At, they are matched to order (At)4. For the standard fourth-order scheme, the constants are assigned the following values:

1 11

в2 = в3 = 2 ’ в4 = 1-0, w1 = w4 = 6 ’ w2 = w3 = 3 • (3.3)

It is known that this choice is not unique. Other choices are possible within the requirement that the Taylor series expansions of Eq. (3.2) are matched to terms of order (At)4. An alternative choice proposed by Hu et al. (1996) called the low – dissipation low-dispersion Runge-Kutta (LDDRK) scheme is widely used in com­putational aeroacoustics (CAA). In formulating the LDDRK scheme, attention is focused on discretizing the time derivative of the convective wave equation,

d u d u

—– + c— = 0,

dt dx

rather than Eq. (3.1). Suppose the spatial derivative of Eq. (3.4) is approximated by a high-order finite difference scheme. The Fourier transform of the finite difference equation is

du __ — = – icau, dt

where u is the Fourier transform of u and a(a) is the wave number of the spatial finite difference approximation of 9/dx.

Now, if the fourth-order RK scheme (3.2) is applied to Eq. (3.5), it is easy to find, after some algebra, that the time marching scheme becomes

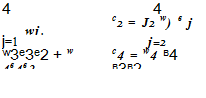
(3.7)

It is a simple matter to show that, for the standard fourth-order RK scheme, Cj = jp
According to LDDRK, the cj constants are assigned the following values:

c1 = 1.0, c2 = 0.5, c3 = 0.162997, c4 = 0.0407574. (3.8)

This choice is motivated by numerical stability consideration and the desire to use the largest At permissible. It turns out that the choice also keeps the numerical dispersion low, as pointed out by Tam (2004). That LDDRK is a low dispersion scheme will be discussed in the next chapter.

To implement the LDDRK scheme, it is necessary to find a set of numerical values of вj and wjs when the cjs are given by Eq. (3.8). A simple way to keep the scheme close to the standard fourth-order scheme is to keep the values of в;- the same as the standard scheme and to determine the values of Wj by solving Eq. (3.7) as a linear system of equations. The values of wj’s are as follows:

W1 = w4 = 0.1630296, w2 = 0.348012, w3 = 0.3259288.