Small-Disturbance Supersonic Flows

The Prandtl-Glauert equation is valid for slender supersonic flows sufficiently far beyond = 1. As a minimum, the flow must be supersonic everywhere, with no locally-subsonic regions. Furthermore, the perturbation velocities must be small enough so the quadratic and higher-order terms in the mass flux ex­pansions (8.44)-(8.46) are much less than unity. Because these also scale as Ы’ф or, the validity of the PG equation becomes restricted to flows which are more and more slender as the Mach number increases. This shrinking range of validity with increasing Mach number is indicated in Figure 8.11.

8.8.1 Supersonic flow analysis problem

The linearized small-disturbance supersonic flow problem has the same governing PG equation and flow – tangency condition as the subsonic case,

but the фхх term now has a negative sign. This fundamentally changes the nature of the solutions, which exhibit waves propagating from the body. It’s also necessary to redefine в so it stays real.

j3 = JM£ — 1 (supersonic flows) (8.129)

8.8.2 2D supersonic airfoil

The wave-like nature of supersonic PG solutions is most easily seen in the 2D thin airfoil case, where we drop фуу and set (nx, ny, nz) = (a-Z, 0 , 1). The PG problem (8.127), (8.128) then simplifies to

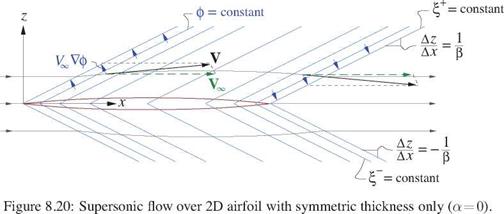
The { functions are called characteristics, along which the solution is constant in this case. Figure 8.20 shows the perturbation velocities and streamlines for the thickness-only case.

The perturbation x-velocities give the pressure coefficients.

c„, – – m,)« – – |[-« + zL+>]

The lift coefficient can then also be computed, assuming the airfoil has Zu — Zi — 0 at x — 0,c.

c£ = j>-Cp n z d(x/c) = J (CPI-CPu)z=0 d(x/c) = I a

Relation (8.136) is the Ackeret equation for 2D supersonic lift. The lift-curve slope is dcg/da = 4/в which can be compared with the 2п/в value on the subsonic side. Interestingly, the supersonic Q is independent of the airfoil shape, since it does not have the q0 camber term of the subsonic case.

The lift can also be obtained from the circulation via the Kutta-Joukowski theorem, which is valid for compressible flows. The circulation is the wake potential jump given by the last form in (8.132).

L’ = p^T = 2T_ = 2 A </>wake = 4^ Ip^VJc СІ4 C fia

Unlike subsonic inviscid 2D airfoils which have zero drag, supersonic inviscid 2D airfoils in general have nonzero wave drag. This is associated with the oblique waves which carry energy away from the airfoil, and hence is different in nature than the wave drag due to a normal shock on subsonic/transonic airfoils which dissipates energy locally. Using the integral momentum theorem on the contour around the airfoil shown in Figure 8.21, we have

DW = – pV■ n (V-V) ■ Xdl ~ – pxV* фг фх nz dl (8.138)

which can in general be separated into wave drag due to lift and wave drag due to thickness.

D

cdw = J 7^- = {Cdjjt + (Cdw)r (8.139)

2 Poo too C

(c-dji = I a2 = c£ a (8.140)

(Cdjr = j5 ^{{Z’J + iZ’^dix/c) (8.141)

It should be noted that all the above results are valid only for thin airfoils at small angles of attack, since

the small-disturbance approximation was used to derive its governing PG equation. An alternative approach is to use Shock-Expansion Theory based on oblique-shock and Prandtl-Meyer expansion-fan functions (see Shapiro [60]). These do not rely on small-disturbance approximations and hence are more accurate, but they do not apply to general 3D flows. Since most practical supersonic applications have low aspect ratios which result in strongly 3D flow, we will restrict our analysis to the PG equation.

Уф ф z