Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
THE DERIVATIVE A„w
 |
This derivative [see (4.12,12)] represents the contribution to the generalized force in the bending degree of freedom, associated with a change in the w velocity of the airplane. A suitable nondimensional form is obtained by defining
and using ax in place of w (w = u0ax). Then the appropriate nondimensional derivative is C&a.
Let the wing lift distribution due to a perturbation a in the angle of attack (constant across the span) be given by Cta{y)a. Then in a virtual displacement in the wing bending mode 8zT, the work done by this wing loading is
(ьп 1 „
 |
SW = — aC, Jy)h(y) 8zT — purely) dy
where c(y) is the local wing chord. The corresponding contribution to 2F is
and to C9a is
(5.10,6)
 |
The tail also contributes to this derivative, for the tail lift associated with a is
and the work done by this force during the virtual displacement is
—a, a
 |
Therefore the contribution to C, f is
and to C9a is
(5.10,7)
The total value of C$n is then the sum of 5.10,6 and 5.10,7.
THE DERIVATIVE bu (see 4.12,12)
This derivative identifies the contribution of zT to the generalized aerodynamic force in the distortion degree of freedom. We have defined the associated wing load distri-
 |
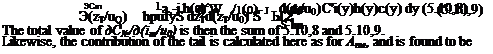bution above by the local lift coefficient Cfy)zT/u0. As in the case of the derivative Anw above, the work done by this loading is calculated, with the result that the wing contributes
5.7 Exercises
5.1 
The derivative C, u contains the term M0
for an airplane with wing loading 70 psf (3,352 Pa) flying at 20,000 ft (6,096 m) altitude, for Mach numbers between 0.2 and 0.8. The following data pertain to the wing:
Sweep (i chord) Л = 30°
S= 5,500 ft2 (511.0 m2)
Plot the result vs. M0. Calculate the contribution this term makes to Z„ and plot this as well. (Compare with Zu for the B747 from Table 6.2, and comment).
5.2 A wind-tunnel model is mounted with one degree of freedom-pivoted so that it can only rotate about the у-axis of the body frame, which is perpendicular to the relative wind. It is elastically restrained with a pitching moment M = —кв. Show how the sum (C,„_( + C,„.) can be estimated from experiments in which the model is free to oscillate in pitch with wind on and off. Assume Mq can be neglected with the wind off and Zq and Zi;. can be neglected.
5.3 Consider the wind/fin system of Fig. 5.16, with the following properties:
Wing: A = 5; A = 0.5; A1/4 = 30°; Г variable
Fin: aF = 3.5 rad-1; lF/b = 0.5; zF/b = 0.1; Vv variable; Эгг/Э/3
negligible.
Estimate values of the stability derivatives (for hnw = h and L/D =12)
c c c c
Wp» ^/r» ^nr
at CUt = 1.0. Plot the spiral stability boundary for horizontal flight:
E — ClrC„, — ClrC,41 = 0
[see (6.8,6) with в0 = 0] in the plane of Vv vs. Г. (Make any reasonable assumptions you need to supplement the given data).
5.4 A jet airplane has a thrust line that passes above the CG by a distance equal to 10% of the M. A.C. With the assumption дТ/ди = 0, estimate the increment thus caused in
a‘ b
![Подпись: 5.5 Find Cn due to the tilting of the lift vector for a wing with an elliptic lift distribution ' l2 4/ i.e., a wing with lift per unit span l(y) which obeys —j H j- = 1 ]. Assume that the](/img/3129/image443_2.gif "THE DERIVATIVE A„w"){kind=small}
tilt angle is small. Express СПр in terms of CL, the lift coefficient of the wing when it is not rolling.
5.6 Assume that Figs. 5.7 and 5.8 are experimental measurements. Select an analytic function CLaJt) that can represent Fig. 5.7 (M = 0 case). Find the corresponding transfer function relating CL to a. Use this transfer function to generate a function of time corresponding to Fig. 5.8b and demonstrate that it has the desired form.
