THE DERIVATIVE C„
The yawing moment produced by the rolling motion is one of the so-called cross derivatives. It is the existence of these cross derivatives that causes the rolling and yawing motions to be so closely coupled. The wing and tail both contribute to Cn .
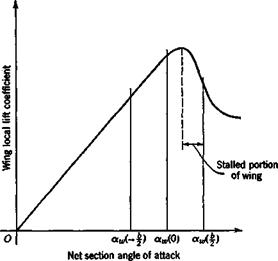
The wing contribution is in two parts. The first comes from the change in profile drag associated with the change in wing angle of attack. The wing a is increased on the right-hand side and decreased on the left-hand side. These changes will normally be accompanied by an increase in profile drag on the right side, and a decrease on the
|
Figure 5.14 Reduction of C, due to wing stall. |
|
|
|
У |
|
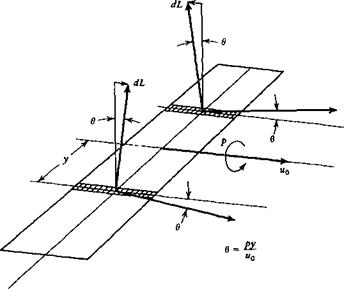
Figure 5.15 Inclination of CL vector due to rolling. |
left side, combining to produce a positive (nose-right) yawing moment. The second wing effect is associated with the fore-and-aft inclination of the lift vector caused by the rolling in subsonic flight and in supersonic flight when the leading edge is subsonic. It depends on the leading-edge suction. The physical situation is illustrated in Fig. 5.15. The directions of motion of two typical wing elements are shown inclined by the angles ± в = py/u0 from the direction of the vector u0. Since the local lift is perpendicular to the local relative wind, then the lift vector on the right half of the wing is inclined forward, and that on the left half backward. The result is a negative yawing couple, proportional to the product CLp. If the wing leading edges are supersonic, then the leading-edge suction is not present, and the local force remains normal to the surface. The increased angle of attack on the right side causes an increase in this normal force there, while the opposite happens on the left side. The result is a positive yawing couple proportional to p.
The tail contribution to СПр is easily found from the tail side force given previously (5.7,2). The incremental C„ is given by
where lF is the distance shown in Fig. 3.12. Therefore
![]()
(5.7,4)
where Vv is the vertical-tail volume ratio.