The Mach-Number Independence Principle of Oswatitsch

We have found in Sub-Sections 6.3.1 and 6.3.2 that for M^ to velocity components, density, Mach number and pressure coefficient behind normal and oblique shocks, and hence behind a bow-shock surface, become indepen­dent of MTO.

We consider now the situation behind a bow-shock surface, for conve­nience only in two dimensions. We use the notation from Fig. 6.9 for the Cartesian velocity components behind a shock surface. We replace in eqs. (6.111) to (6.113), (6.70), (6.103), and (6.105) the subscript 1 with to, write

parameters non-dimensionalized with their free-stream parameters[77]

Experimental observations, and these relations have led to what we call Oswatitsch’s Mach number independence principle.[78] In his original work, [44], Oswatitsch defines flow at very large Mach numbers M ^ 1 as hy­personic flow, see also [22]. All flows at large Mach numbers have already hypersonic properties in the sense that certain force coefficients become in­dependent of the Mach number. This happens, depending on the body form, already for free-stream Mach numbers as low as Mto = 4 to 5, see for instance Fig. 6.40.[79]

For practical purposes we hence can say that Mach number independence is given, if for a given body in a steady free stream the shape of the bow-shock surface, the streamline pattern, the sonic surface, the Mach lines (character­istics) in the supersonic part of the flow field, the pressure coefficient, as well as the force and moment coefficients asymptotically become Mach number independent. This holds for inviscid perfect gas flow. Below we will come back to the principle for the cases of viscous and high-temperature real-gas flows.

We consider here in particular the case of blunt bodies. This relates mainly to RV’s, but also to high flight Mach number CAV’s, which always have a

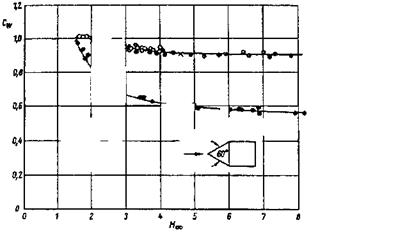o — Charters and Thomas ft — Hodges • — Stevens x ■= Naumann

nose with finite bluntness in order to withstand the thermal loads at large flight speeds.

The shape of the bow-shock surface is governed by the body shape and the free-stream parameters. The flow properties just behind the bow-shock surface are the upstream boundary conditions for the flow past the body. For Mж ^ ж they are those given in eqs. (6.168) to (6.171). They are functions of the shape of the bow-shock surface, i. e., the shock angle в, and the ratio of specific heats 7.

In the following we consider still only the two-dimensional case. This suffices completely to show the essence of the Mach-number independence principle. The derivation of the general three-dimensional case is straight forward.

We derive first the gasdynamic equation. We consider steady inviscid flow of a perfect gas. We re-formulate the pressure-gradient terms of the Euler equations—in two dimensions eqs. (4.27) and (4.28) without the molecular and mass-diffusion transport terms—with the speed of sound, eq. (6.8)

dp = dP = °2dp-

We combine now the Euler equations with the continuity equation eq. (4.83), neglect the time derivatives, and find the gasdynamic equation in two-dimensional Cartesian coordinates

dv

— + uv dy
du dv dy dx

Together with Crocco’s theorem

V x rotV_= — T grads, (6.176)

we have three equations for the determination of u, v, and the entropy s.

To eliminate the speed of sound a and the temperature T we use eq. (6.14). We rewrite that equation and find with V2 = u2 + v2 (see Fig. 6.9):

The question is whether indeed the terms with 1/M2 can be omitted, because at slender bodies V « иж, and hence 1 — (V2/u2) is small, too. It is argued that V/uж depends only on the shock angle of the bow shock, eq. (6.170), and not on Мж [44]. Therefore eqs. (6.180) and (6.179) are suf­ficiently exact, as long as Мж is sufficiently large.

It remains the problem to express in eq. (6.176) the entropy s for Мж ^ ж. From eq. (6.79) for the normal shock surface we gather that in this case s ^ ж, which also holds for an oblique shock surface. This problem is circumvented by introducing the difference s’ = soblique shock – Snormal shock:[80]

2y cv

These equations describe the flow between the bow-shock and the body surface. They are supplemented by the boundary conditions behind the bow – shock surface, eqs. (6.168), (6.169) (6.182), and the boundary conditions at the body surface. The latter are kinematic conditions, which demand vanish­ing of the flow-velocity component normal to the body surface, i. e., the flow to be tangential to it.

The system of equations is independent of the free-stream Mach number MTO. Assuming uniqueness, we deduce from it that u’, v’ and s’ in the flow field between bow-shock surface and body surface do not depend on MTO, but only on the body shape, and the ratio of specific heats y. This holds also for the shape of the bow-shock surface, and the pattern of the streamlines, the sonic line, and the Mach lines in the supersonic part of the flow field. Density p’, eq. (6.171) and pressure coefficient cp, eq. (6.173), and with the latter the force and moment coefficients, are also independent of MTO.[81]

Oswatitsch called his result a similarity law. In [22] it is argued that to call it “independence principle” would be more apt, because it is a special type of similitude, being stronger than a general similitude. It is valid at the windward side of a body, i. e., in the portions of the flow past a body, where the bow-shock surface lies close to the body surface, see, e. g., Fig. 6.22 b). It is not valid at the leeward side of a body, where, due to the hypersonic shadow effect, only small forces are exerted on the body surface. Nothing is stated about transition regimes between windward side and leeward side surface portions.

In [44] no solution of the system of equations (6.183) and (6.184) is given. A recent solution can be found in [45]. In [22] several theories are discussed, some of which base directly on the findings of Oswatitsch. We have used results of two of these theories in Sub-Section 6.4.1 to discuss the influence of high-temperature real-gas effects on the bow-shock stand-off distance at a blunt body.

Oswatitsch’s independence principle is an important principle for applied aerothermodynamics. If we obtain for a given body shape experimentally for instance the force coefficients at a Mach number M^ large enough, they are valid then for all larger Mach numbers Mo > M^, Fig. 6.40, provided, however, that we have perfect-gas flow.[82] In [22] it is argued that Oswatitsch’s independence principle also holds for non-perfect gas flow. In any case we can introduce an effective ratio of specific heats Yef f, and thus study the influence of high-temperature real-gas effects.

In [2] this is made in view of the pitching moment anomaly observed during the first re-entry flight of the Space Shuttle Orbiter. Together with results of solutions of the Euler equations it is shown that obviously a “be­nign” (inviscid) wall Mach number interval exists with Mwau ^ 2.2 in which high-temperature real-gas effects only very weakly violate the Mach number independence principle. Above that wall Mach number it begins to lose its validity.

In [22] it is claimed too, that the principle holds for boundary layers in hypersonic flows, as long as the external inviscid flow follows the independence principle. In [46] results of a numerical study are given which indicate that this holds only in the case of an adiabatic wall and in any case not for a radiation or otherwise cooled wall.

For slender, sharp-nosed bodies at very large Mach numbers Mo the Mach angle /i, o may be of the same order of magnitude as the maximum deflection angle в, which the flow undergoes at the body surface. This class of high Mach number flow is characterized by the hypersonic similarity parameter, see, e. g., [4, 6]

K = Mo sin в ^ 1, (6.185)

which was introduced by Tsien [47].[83]

In terms of the thickness ratio т (body thickness/body length) of such bodies it reads

K = Mot > 1. (6.186)

Not going into details of the theory we note the results [4, 44], which are important for aerodynamic shape definition:

— the surface pressure coefficient of a body with thickness ratio т follows

cp ж т2, (6.187)

— and the wave drag coefficient

CDw ж т3. (6.188)

It can be expected that these results give also the right increments in the case of slender, blunt-nosed configurations at small angle of attack, i. e., CAV’s. Of course at a blunt nose (the nose bluntness is the major driver of the wave drag) the pressure coefficient is not covered by the relation (6.187).