VARIABLES

Approximate solutions to the exact potential flow problem are obtained in this book using both classical small-disturbance methods and numerical modeling. It is important to have exact solutions available to test the accuracy of the approximations and to assess their applicability. In this chapter complex variables will be used to obtain the solution to three model problems: the flat plate, the circular arc, and a symmetrical airfoil.

6.1 SUMMARY OF COMPLEX VARIABLE THEORY

Prior to applying complex variable methods to potential flow problems, some of the principles are discussed briefly (for more details about the mathematics of complex variables, see Churchill6л). To begin, first define the imaginary unit

і by

;2=-i (6.1)

Then any complex number У can be written as

Y = a + ib (6.2)

where a and b are real and are called the real and imaginary parts of Y,

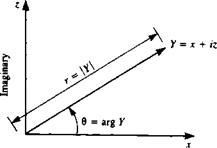respectively. Every complex number therefore can be thought of as repre­senting an ordered pair of real numbers {a, b) and as such may be represented geometrically by points in a plane. The complex number У = x + iz is shown in Fig. 6.1 in a cartesian coordinate system with x and z axes. A polar coordinate version of Y with coordinates r and Q is also shown in the figure. Note that the absolute value of Y (|У|) is defined as л/х2 + z2 and the argument of У (arg У = в) is defined as tan-1 z/x. An exponential form of У is expressed as

Y = reie (6.3)

if the exponential term is defined as

cos 0 + i sin 6 = e, e (6.4)

The complex conjugate of the complex number У is defined as

Y = x — iz

Otherwise the algebra of complex numbers is similar to the algebra of the term (a + b), but note that i2 = — 1. As an example, the multiplication of a complex number by its conjugate is

YY = (x + iz){x-iz)=x2 + z2

A function / of the complex variable У can be written in terms of its real and imaginary parts as

f(Y) = g(x, z) + ih(x, z) (6.5)

Analytic functions of a complex variable are differentiable, which means that

= Hm /(У+АУ)-/(У) dY ду – о ДУ

exists for all possible paths АУ. Now consider the derivative of f(Y) along the x axis

df(Y) |jm Ag + iAh_3g ^dh dY д*—о Ax Эх Эх

Similarly, the derivative in the z direction is

df(Y) bg + ibh 1 dg dh dh. dg

—— = lim ————— — ~ ——I – —~ ~— і ~r~

dY /Аг—о 1 Az 1 dz dz dz dz

The derivatives must be independent of the direction of differentiation; therefore, equating the real and imaginary parts of these derivatives results in

3g_3h 3e = _Sh (66)

dx dz dz dx

So, differentiability is guaranteed if the real and imaginary parts of/satisfy the above equations, which are called the Cauchy-Riemann conditions. Also, if a function of a complex variable is analytic, then the real and imaginary parts each satisfy Laplace’s equation. Points in a region where /(У) is analytic are called regular points and points where f(Y) is not analytic are called singular points.

Consider the integration of a complex function. If the function is analytic and the region is simply connected, then the integral

from point A to point В is independent of the path of integration and the integral around all closed paths is zero. The latter result is called the Cauchy Integral Theorem. Multiply connected regions are of interest since they include the region exterior to a two-dimensional airfoil as well as the region remaining once singular points are excluded by surrounding them with closed curves. Consider the region in Fig. 6.2 that is exterior to n curves Clt C2, ■ ■ ■, Cn and consider a curve C that surrounds the n curves. An application of the Cauchy Integral Theorem in this region for a function / that is analytic inside C and outside the n curves yields the result that the integral around C is equal to the sum of the integrals around the n curves where all of the internal integrations are in the same direction:

j>f(Y)dY = f f(Y)dY + j> f(Y)dY+-■- + j> f(Y)dY (6.7)

Consider the following results for power series expansions of the function f(Y). If / is analytic at all points within a circle C0 with center at Y0, then at each point У inside the circle / can be represented by the Taylor series expansion

f(Y) =/(У0) +/'(У0)(У – Уо) + ■ • (У – УоГ + • • • (6.8)

n

Now consider the region exterior to the circle Ci whose center is at У0 in Fig. 6.3. The function / is analytic in the annular region between C, and C2.

Then / can be represented by the Laurent series expansion

f(Y) = ?,An(Y-Y0y (6.9)

—oo

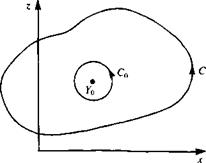
Consider now the integration of a function with singularities. Let /(Y) be analytic inside the curve C except at Y0. Surround Y0 by the circle C„ (see Fig. 6.4) and represent/between C0 and C by the Laurent series of Eq. (6.9). Then the integral around C becomes

<j> /(Y) dY = І aA (Y – Yo)" dY = 2ліА-і (6.10)

Jc – oo JcB

where A-t is the coefficient of the term Л_,/(У — Y0) and is called the residue of f(Y) at Y0. If /(Y) is analytic inside C except at a finite number of singularities (N), then a generalization of Eq. (6.10) leads to the Residue Theorem:

lf(Y)dY = 2m%A-l(Yj) Jc /=1

FIGURE 6.4

Integration of a function with singularities.

FIGURE 6.5 Mapping with a function of a complex variable.

Complex variable theory is a powerful tool for the solution of two – dimensional incompressible potential flow problems through its mapping properties. Consider the function f(Y), that generates the pair of values (g, h) for each pair of values (x, z). Each value of У represents a point in the Y plane and each value of / can be thought of as representing a corresponding point in the / plane. The function f(Y) therefore geometrically maps or transforms points (and also curves and regions) from the У plane to the / plane (see Fig.

6.5) .

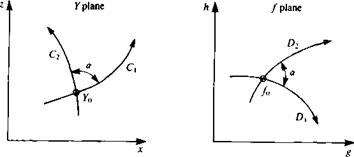
When the mapping function /(У) is analytic, the mapping from the У plane to the f plane is called conformal and has the following special property. Consider a curve C through the point Y0 in the У plane and the corresponding curve D through the corresponding point f0 in the / plane (Fig. 6.6). If / is analytic at!<, and if f'(Y0) Ф 0 then every curve through lo in the У plane is rotated by the amount arg/'(y0) when it is transformed into the /plane. This is illustrated in Fig. 6.6, which shows the two curves Cx and C2 that intersect at У0 in the У plane and the corresponding curves D, and D2 that intersect at f0 in the f plane. For this conformal mapping, it is observed that the angle of intersection between the curves is preserved in the transformation. A point at

FIGURE 6.6 Preservation of the angle between intersecting curves for a conformal transformation.

which f'(Y) = 0 is called a critical point of the mapping and at a critical point the above intersection angle is not preserved.