Vortex sheets

To estimate the influence of the near wake on the aerodynamic characteristics of a lifting wing it is useful to investigate the ‘hypothetical’ bound vortex in greater detail. For this the wing is replaced for the purposes of analysis by a sheet of vortex

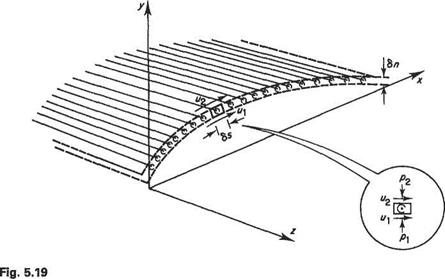
filaments. In order to satisfy Helmholtz’s second theorem (Section 5.2.1) each fila­ment must either be part of a closed loop or form a horseshoe vortex with trailing vortex filaments running to infinity. Even with this restriction there are still infinitely many ways of arranging such vortex elements for the purposes of modelling the flow field associated with a lifting wing. For illustrative purposes consider the simple arrangement where there is a sheet of vortex filaments passing in the spanwise direction through a given wing section (Fig. 5.19). It should be noted, however, that at two, here unspecified, spanwise locations each of these filaments must be turned back to form trailing vortex filaments.

Consider the flow in the vicinity of a sheet of fluid moving irrotationally in the xy plane, Fig. 5.19. In this stylized figure the ‘sheet’ is seen to have a section curved in the xy plane and to be of thickness 8n, and the vortidty is represented by a number of vortex filaments normal to the xy plane. The circulation around the element of fluid having sides 8s, 8n is, by definition, ДГ = (8s. 8n where (is the vorticity of the fluid within the area 8s 8n.

Now for a sheet 8n -* 0 and if (is so large that the product (8n remains finite, the sheet is termed a vortex sheet of strength к = (8n. The circulation around the element can now be written

AT = k8s (5.21)

An alternative way of finding the circulation around the element is to integrate the tangential flow components. Thus

ДГ = (m2 — ui)8s (5.22)

Comparison of Eqns (5.21) and (5.22) shows that the local strength к of the vortex sheet is the tangential velocity jump through the sheet.

Alternatively, a flow situation in which the tangential velocity changes discontinu­ously in the normal direction may be mathematically represented by a vortex sheet of strength proportional to the velocity change.

The vortex sheet concept has important applications in wing theory.