7.8 THE V DERIVATIVES (CTv, CDy, CLp, Cmr, Chep)

This group of derivatives gives the changes that occur in the coefficient when the flight speed V changes, while the other variables, i. e. a, q, zE, de, remain constant. It is important to remember that the propulsion controls (e. g. the throttle) are also kept fixed.

THE DERIVATIVE CTy

The derivative 0Ty depends on the type of propulsion system, specifically on how T varies with V at fixed throttle. In general it is given by

(дТ/дУ)е 2 Te

iPVe8 і PV*8

^Ш-2СТ

PVeS

For constant-thrust propulsion, as for jet and rocket engines, dTjdV — 0

and j —■ —2G rp

For constant-power propulsion, TV = const, whence

TdV+ VdT = 0

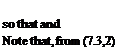ldJL = _ L.

w)e re

CTr=-ZCTe (7.8,2)

__ /Gn + Gl tan y

‘ 1 — aT tan у Je

For piston-engine-propeller systems, the usual fixed-control case implies fixed throttle and constant RPM. In that case the brake horsepower is constant, and the thrust is given by

TV = VPB

have	TdV + VdT = PB dr]
or	/3 T T PB/dr, dv)e ve ve dvh	(7.8,4)
and	GT — 3CT + Pp i3*1) F dvje

where rj = propulsive efficiency and PB is the engine shaft power. We then

After substituting for PB from (7.8,3) we get

This relation is useful, since the variation of t] with V would normally he known for a propeller-driven airplane.

THE DERIVATIVE CDy

In order to include all the main effects of speed changes formally, we shall assume that the drag coefficient is a function of Mach number M, the dynamic pressure

Pd = iPV2 (7.8,6)

and the thrust coefficient, i. e.

Gj) = GB( Pa> @t)

Since M = V/a, where a is the speed of sound, then

ЭМ 1 3pa 3 CT

^F = _; ы=р7 and

oV a oV oV

The aeroelastic effect on CDy (the pa term) is not likely to be large enough to need to be included in other than exceptional cases.