Analysis of the Flow Past a Given Rotor

In this section we consider the problem of calculating the flow past a given rotor. This is particularly useful to assess the performance of an optimum rotor at off-design conditions. Here, the blade sections will have variable working conditions in terms of a(y), with the possibility, on part of the blade, for the incidences to be larger than the incidence of maximum lift, i. e. a > (a)Clmax. In other words, part of the blade may be stalled. This will typically happen at small TSR’s.

10.5.1 Formulation

With reference to Fig. 10.11, given a data set {CdVm, Cm, am} that characterizes the blade profile viscous polar, the governing equation simply reads

where a(y) = ф(у)—ї (y). The chord c( y) and twist t (y) distributions are given. The incoming velocity is q(y) = ^(1 + u(у))2 + (-3у – + w(y))2 and Г is the unknown circulation (Г < 0). In discrete form this reads

1

Г = – qjCjCi (a j), j = 2,…, jx – 1 (10.89)

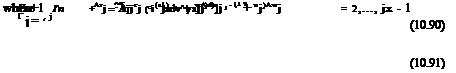
When a j < (a)Clmax, then <yCL > 0 and the simple, partial Newton linearization gives a converging algorithm

Auj and Awj are given by the induced velocity coefficients associated with Arj = Г]п+1 – Гj.

m is the relaxation factor and can be chosen up to m = 1.8. It is found that the coefficients aj, j – aj_i, j + aj, j < 0 and Cj, j – Cj_i, j > 0 so that the linearization contributions reinforce the diagonal of the iterative matrix underlying the relaxation method [11]. With jx = 101 this typically converges in a few hundreds of iterations.